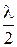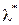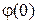КОНСПЕКТ ЛЕКЦІЙ
“Методи оптимізації та дослiдження операцiй”
за фахом «Програмна інженерія»
факультету №9
Харків – 2011
Применение метода наискорейшего спуска для решения задачи минимизации без ограничений было рассмотрено еще известным французским математиком Коши. Как известно из курса математического анализа, градиент целевой функции 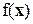 в любой точке
в любой точке
x=(x1,…,xn) есть вектор в направлении локального увеличения 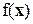 . Следовательно, для минимизации целевой функции нужно двигаться в направлении, противоположном градиенту
. Следовательно, для минимизации целевой функции нужно двигаться в направлении, противоположном градиенту 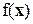 , т.е. в направлении наискорейшего спуска, поскольку отрицательный градиент
, т.е. в направлении наискорейшего спуска, поскольку отрицательный градиент 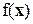 в точке
в точке 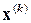 =(x1 (k) ,…,xn (k) ) направлен в сторону наибольшего уменьшения
=(x1 (k) ,…,xn (k) ) направлен в сторону наибольшего уменьшения 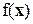 по всем компонентам x и ортогонален линии уровня
по всем компонентам x и ортогонален линии уровня 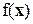 в точке
в точке 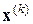 , где k – номер шага метода, k=0, 1, …. Введение направления, противоположного градиенту, т.е. направления наискорейшего спуска, дает следующую формулу перехода из
, где k – номер шага метода, k=0, 1, …. Введение направления, противоположного градиенту, т.е. направления наискорейшего спуска, дает следующую формулу перехода из 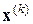 в
в 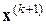 :
:
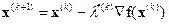 (3.1.1)
(3.1.1)
Отрицательный градиент дает только направление оптимизации, но не величину шага. При этом можно использовать различные версии метода наискорейшего спуска в зависимости от процедуры выбора 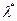 . Поскольку один шаг в направлении наискорейшего спуска в общем случае не приводит в точку минимума
. Поскольку один шаг в направлении наискорейшего спуска в общем случае не приводит в точку минимума 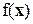 , формула (3.1.1) должна применяться несколько раз до тех пор, пока минимум не будет достигнут. В точке минимума все сотавляющие вектора градиента равны нулю, т.е. критерий останова алгоритма поиска:
, формула (3.1.1) должна применяться несколько раз до тех пор, пока минимум не будет достигнут. В точке минимума все сотавляющие вектора градиента равны нулю, т.е. критерий останова алгоритма поиска:
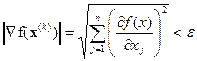 (3.1.2)
(3.1.2)
Используем следующий метод нахождения 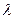 . Пусть
. Пусть 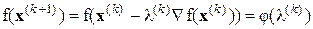 - функция от
- функция от 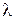 . Наращиваем
. Наращиваем 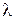 от 0 с малым шагом до тех пор, пока не получим
от 0 с малым шагом до тех пор, пока не получим 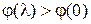 .
.
Построим полином второго порядка для 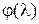 по трем точкам (0,
по трем точкам (0, 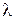 /2,
/2, 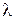 ):
):
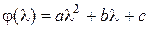 , где
, где 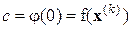 . (3.1.3)
. (3.1.3)
Составляем систему:
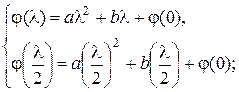 (3.1.4)
(3.1.4)
|

|
|
|
|
|
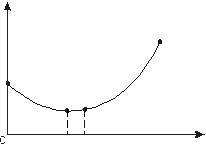
решаем ее относительно коэффициентов a и b, после чего находим оптимальное значение 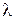 как координату экстремума параболы
как координату экстремума параболы 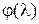 по формуле:
по формуле:
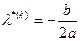 . (3.1.5)
. (3.1.5)
Для вычисления градиента функции воспользуемся определением производной 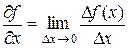 , пусть
, пусть 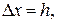
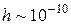 , тогда
, тогда
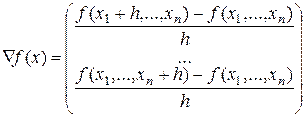 (3.1.6)
(3.1.6)
Таким образом, используя формулы (3.1.1)-(3.1.6), получаем минимизирующую последовательность и искомое значение 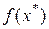 .
.
 2014-02-24
2014-02-24 621
621