Д о к а з а т е л ь с т в о. Нетрудно показать, что любая точка многогранника является выпуклой комбинацией его вершин. Тогда и точка 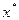 , в которой функция
, в которой функция 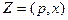 достигает экстремума (пусть, например, минимума) представима в виде
достигает экстремума (пусть, например, минимума) представима в виде
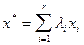 ,
, 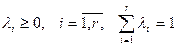 ,
,
где 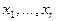 - вершины многогранника W.
- вершины многогранника W.
В силу линейности 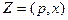 имеем
имеем
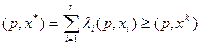 , (3.9)
, (3.9)
где 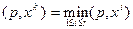 .
.
Проиллюстрируем справедливость правой части (3.9) на примере двух точек:
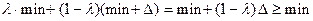 .
.
Но, по предположению, 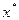 - оптимальное решение, следовательно
- оптимальное решение, следовательно  , т.е. существует вершина
, т.е. существует вершина 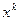 , в которой линейная форма принимает минимальное значение.
, в которой линейная форма принимает минимальное значение.
Для максимума доказательство аналогично.
Рассмотрим геометрическую интерпретацию для двумерного пространства. Здесь многогранник W является многоугольником, гиперплоскости 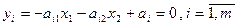 - прямыми, а полупространства
- прямыми, а полупространства 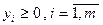 - полуплоскостями (на рисунках их будем определять штриховкой в сторону выполнения неравенств). Ясно, что решением ОЗЛП будет какая-то вершина многоугольника W. На Рис. 3.1а решение задачи максимизации формы
- полуплоскостями (на рисунках их будем определять штриховкой в сторону выполнения неравенств). Ясно, что решением ОЗЛП будет какая-то вершина многоугольника W. На Рис. 3.1а решение задачи максимизации формы 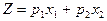 дает вершина Р1, а задачи минимизации - вершина Р2, причем эти решения единственны. Случай существования бесчисленного множества решений иллюстрирует Рис. 3.1b. Случай неограниченности функции Z на W показан на Рис. 3.1c, случай отсутствия решения - Рис. 3.1d (многогранник решений - пустое множество, система ограничений несовместна).
дает вершина Р1, а задачи минимизации - вершина Р2, причем эти решения единственны. Случай существования бесчисленного множества решений иллюстрирует Рис. 3.1b. Случай неограниченности функции Z на W показан на Рис. 3.1c, случай отсутствия решения - Рис. 3.1d (многогранник решений - пустое множество, система ограничений несовместна).
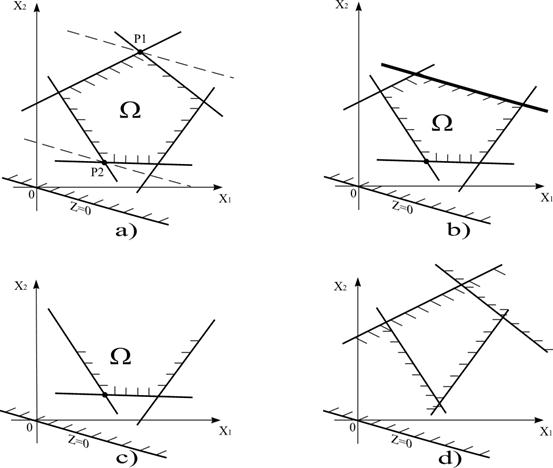
Рис. 3.1.
Лекция 4. Симплекс-метод решения ОЗЛП
Основным методом решения задач линейного программирования является так называемый симплекс-метод, основоположником которого является американский ученый Дж. Данциг.
Симплекс-метод состоит из алгоритма отыскания опорного решения системы линейных неравенств (3.2), т.е. определения координат любой вершины многогранника W (или установления факта несовместности системы), и алгоритма направленного перехода от полученного опорного решения к оптимальному - вершине с максимальным (минимальным) значением функции цели (3.1). Основу вычислительной схемы симплекс-метода составляют МЖИ.
Л4.1. Переход к таблице
Функцию цели (3.1) и условия (3.2) записываются в виде следующей таблицы:
| ... | 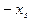
| ... | 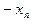
| ||
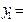
| 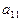
| ... | 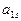
| ... | 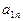
| 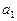
|
| ... | . | . | . | . | . | ... |
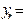
| 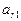
| ... | 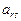
| ... | 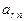
| 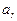
|
| ... | . | . | . | . | . | ... |
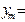
| 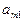
| ... | 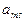
| ... | 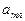
| 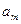
|
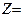
| 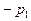
| ... | 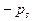
| ... | 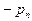
|
(4.1)
Если среди ограничений (3.2) встречаются ограничения лишь на знак переменной, т.е. 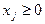 , то их не включают в таблицу (4.1). Если
, то их не включают в таблицу (4.1). Если 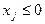 , то в системе (3.1)-(3.2) делается замена переменных
, то в системе (3.1)-(3.2) делается замена переменных 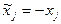 , и ограничение
, и ограничение 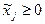 также в таблицу не включается.
также в таблицу не включается.
Переменные, на знак которых наложено ограничение, называются несвободными, остальные - свободными.
Верхние переменные таблицы называются базисными, левые - зависимыми. Последний столбец будем называть столбцомсвободных членов, нижнюю строку - Z-строкой. Каждой таблице вида (4.1) геометрически будет соответствовать точка таблицы - начало координат пространства, определяемого базисными переменными.
Л4.2. Исключение свободных переменных
Для простоты изложения будем считать, что все переменные 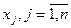 свободны и что ранг матрицы
свободны и что ранг матрицы 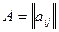 коэффициентов системы (3.2) равен
коэффициентов системы (3.2) равен 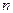 . Тогда (см. Л2.3.) с помощью
. Тогда (см. Л2.3.) с помощью 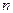 МЖИ можно перевести
МЖИ можно перевести 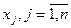 из верхней строки таблицы в ее левый столбец и на их место поставить соответствующие
из верхней строки таблицы в ее левый столбец и на их место поставить соответствующие 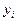 . При этом в классической постановке метода никаких ограничений на выбор разрешающих элементов не налагается, лишь бы они были отличны от нуля.
. При этом в классической постановке метода никаких ограничений на выбор разрешающих элементов не налагается, лишь бы они были отличны от нуля.
Для удобства записи можно считать, что на верх таблицы перешли 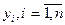 , так что получена таблица вида:
, так что получена таблица вида:
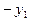
| ... | 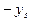
| ... | 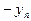
| ||
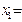
| 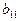
| ... | 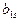
| ... | 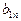
| 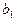
|
| ... | . | . | . | . | . | ... |
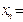
| 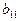
| ... | 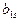
| ... | 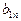
| 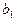
|
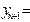
| 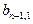
| ... | 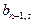
| ... | 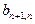
| 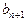
|
| ... | . | . | . | . | . | ... |
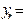
| 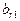
| ... | 
| ... | 
| 
|
| ... | . | . | . | . | . | ... |
| 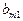
| ... | 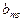
| ... | 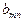
| 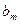
|
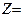
| 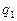
| ... | 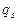
| ... | 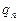
| 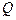
|
Выражения для переменных 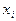
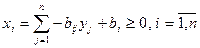
выписываются из таблицы отдельно (они понадобятся лишь после получения решения, чтобы выразить его в старом базисе).
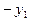
| ... | 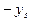
| ... | 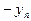
| ||
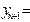
| 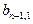
| ... | 
| ... | 
| 
|
| ... | . | . | . | . | . | ... |
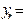
| 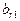
| ... | 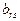
| ... | 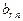
| 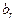
|
| ... | . | . | . | . | . | ... |
| 
| ... | 
| ... | 
| 
|
| 
| ... | 
| ... | 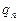
| 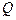
|
Далее продолжаем работать с оставшейся частью таблицы:
. (4.2)
Так как по условию (3.2) 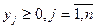 то переходим к следующей обычной формулировке ЛП-задачи (например максимизации):
то переходим к следующей обычной формулировке ЛП-задачи (например максимизации):
 2014-02-24
2014-02-24 467
467








