Теорема 3.1. Пусть множество выпукло. Тогда выпуклая комбинация произвольного количества точек этого множества принадлежит этому множеству

Д о к а з а т е л ь с т в о. Пусть 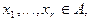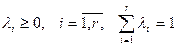. Покажем, что .

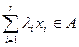Доказательство проведем методом математической индукции. Для 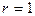теорема очевидна. Для 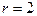теорема справедлива по определению выпуклого множества.

Предположим, что теорема справедлива для 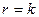, т.е.

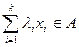. (3.4)

Докажем, что теорема верна и для 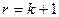, т.е.

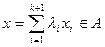. (3.5)

Можно предположить, что в (3.5) 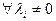, так как в противном случае теорема верна по предположению. Поскольку 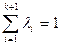, то .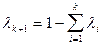

Обозначая 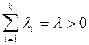, имеем. Теперь

.

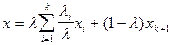Поскольку 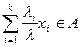в силу (3.4), 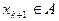по условию, то по определению выпуклого множества 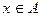, что и требовалось доказать.

Пересечением двух множеств 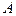и 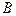называется такое множество 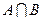, которое состоит из точек, принадлежащих одновременно как 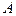, так и .

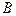Полупространством в 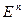называется множество точек 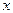, удовлетворяющих соотношению

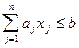, (3.6)

где 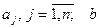- некоторые константы.

Гиперплоскостью называется множество точек 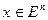, удовлетворяющих линейному уравнению

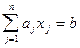. (3.7)

Любая гиперплоскость (3.7) может быть представлена как пересечение двух полупространств

, .

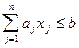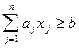Многогранным множеством называется пересечение конечного числа полупространств. Ограниченное многогранное множество называется многогранником.

Каждое из неравенств системы (3.2) определяет полупространство. Соответственно, допустимое множество W, определяемое системой (3.2), является (если оно не пусто) многогранным множеством.

Покажем, что многогранное множество W выпукло.