Теорема 3.2. Полупространство является выпуклым множеством

Д о к а з а т е л ь с т в о. Пусть 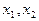- две точки полупространства (3.6), т.е.

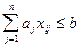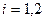, (3.8)

Покажем, что точка 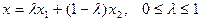, также принадлежит полупространству, т.е. удовлетворяет (3.6). Действительно, в силу (3.8) получаем

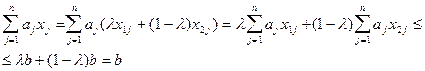
Теорема доказана.

Теорема 3.3. Пересечение двух или более выпуклых множеств является выпуклым.

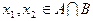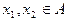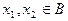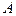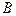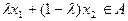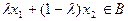Д о к а з а т е л ь с т в о. Пусть . По определению пересечения и . Так как и выпуклы, то и , где .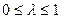

Следовательно, 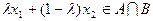, что и требовалось доказать.

Следствие. Гиперплоскость является выпуклым множеством.

Из приведенных определений и доказанных теорем вытекает следующее утверждение.