Доказательство. В доказательстве будем использовать символ Кронекера

В доказательстве будем использовать символ Кронекера:

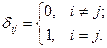
Положим:

,

т.е. 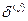- точка пространства E^m, 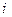-я координата которой равна 1, а остальные - 0.

Положим также:

,

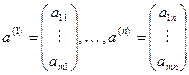т.е. 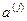- точки пространства E^m, координаты которых - столбцы матрицы А.

Пусть D - выпуклая оболочка множества m+n точек

.

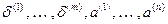Пусть Z=(0,...,0) - начало координат E^m.

Разберем 2 случая: ZÎD, и ZÏD.

Если ZÎD, то Z - выпуклая линейная комбинация точек 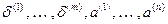, т.е. существует элемент 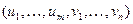множества S_n+m такой, что

,

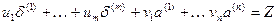или .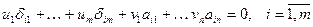

Следовательно: .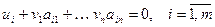

Т.к. 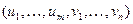ÎS_n+m, то 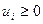и .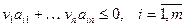

Заметим, что 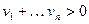, т.к. иначе (=0) 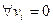и 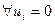, чего не может быть.

Поэтому положим:

.

Очевидно, что вектор yÎS_n и 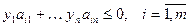, т.е. условие (2) леммы выполняется.

Пусть ZÏD.

Тогда, очевидно, существует гиперплоскость 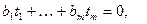проходящая через начало координат пространства E^m (содержащая точку Z), такая, что D находится в положительном полупространстве - для любой точки 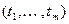ÎD справедливо неравенство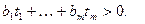

Тогда точки 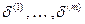области D также удовлетворяют этому неравенству: 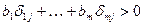. Т.е. .

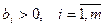Кроме того, это неравенство справедливо также и для точек

: ,.

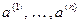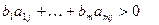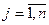Положим:

.

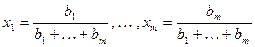Очевидно, что вектор xÎS_m и 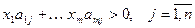. Тогда и подавно , т.е. условие (1) леммы выполняется.

Основная теорема для прямоугольных игр (теорема фон Неймана)

Пусть 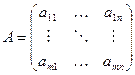- некоторая матрица, и пусть математическое ожидание выигрыша 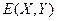для любого 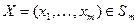и любого 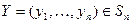определено следующим образом: .

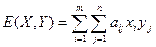Тогда величины 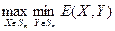и 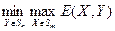существуют и равны между собой.