Лекция № 11-12
Список используемой литературы
- Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.1. – М.: ОНИКС. 2003. – 304 с.
- Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.2. – М.: ОНИКС. 2003 – 415 с
- Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с
- Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.
- Колесников, А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М.,2001, - 208 с.
- Кремер, Н.Ш. Высшая математика для экономистов: Учебник для вузов. - М.: ЮНИТИ, 2004. – 471 с.
Тема «Производная»
Цель: изучитьосновные теоремы дифференциального исчисления, правило Лопиталя, научить применять производную для исследования функций.
Ключевые слова: непрерывная функция, дифференцируемая функция, радиент.
Вопросы:
1. Основные теоремы дифференциального исчисления.
2. Правило Лопиталя.
3. Производные высших порядков.
4. Исследование функций и построение их графиков.
5. Приложение производной в экономике.
1) непрерывна на [a;b],
2) дифференцируема в интервале (a;b),
3) на концах интервала функция принимает равные значения т.е. f(а)= f(b)
тогда внутри отрезка существует по крайней мере одна такая точка 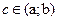 , в которой производная функции равна нулю:
, в которой производная функции равна нулю: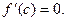
Если 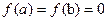 , то говорят, что между двумя последовательными нулями дифференцируемой функции, имеется хотя бы один нуль ее производной, т.е.
, то говорят, что между двумя последовательными нулями дифференцируемой функции, имеется хотя бы один нуль ее производной, т.е. 
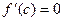 .
.
Теорема Лагранжа. Пусть функция y= f(x) удовлетворяет следующим условиям:
1)непрерывна на [a;b]
2)дифференцируема на (a;b),
тогда существует такая точка 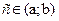 , что -
, что - 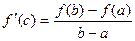
 |
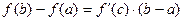 - формула Лагранжа или формула конечных приращений.
- формула Лагранжа или формула конечных приращений.
Геометрически теорема Лагранжа означает, что на кривой АВ найдется точка М(с;f(с)) в которой касательная параллельна хорде АВ.
Теорема Лагранжа дает возможность установить признаки постоянства, возрастания и убывания функции.
Теорема Коши. Если функции 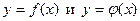 непрерывны на [a;b] и дифференцируемы в (a;b), причем
непрерывны на [a;b] и дифференцируемы в (a;b), причем 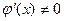 , тогда существует такая точка
, тогда существует такая точка 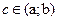 ,что справедлива формула
,что справедлива формула 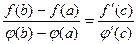 .
.
 2014-02-24
2014-02-24 1045
1045








