1.Рассмотрим сначала интегралы вида
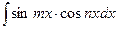 ,
, 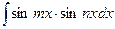 ,
, 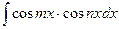 .
.
Воспользовавшись известными тригонометрическими формулами:
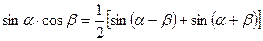
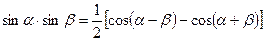
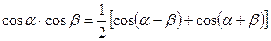
можно преобразовать каждое из произведений под знаком интеграла в алгебраическую сумму и проинтегрировать по табличным формулам.
Пример. Найти: 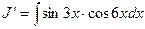
Решение. 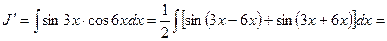
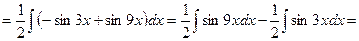
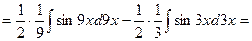
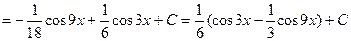
II. Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.
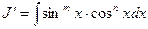
В частных случаях один из показателей (m или n) может равняться нулю.
Пусть m и n – целые неотрицательные числа.
Здесь различают два случая:
а) хотя бы один из показателей m и n есть число нечетное
б) оба показателя m и n – числа четные
В первом а) случае интеграл берется непосредственно, отделяя от нечетной степени один множитель и полагая кофункцию этого множителя равной новой переменной t.
Пример. 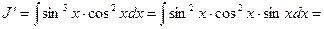
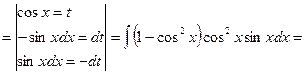
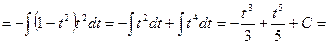
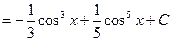
Во втором б) случае для вычисления интеграла используются формулы понижения степени
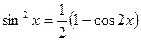 ,
, 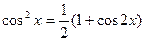 ,
, 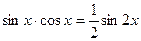
Пример. 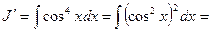
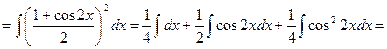
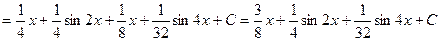
 2014-02-24
2014-02-24 679
679








