Пример.
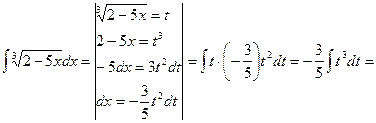
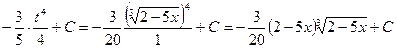
Не существует формулы, выражающей интеграл от произведения функций через интегралы от сомножителей.
Пусть u=u(x) и v=v(x) – непрерывно дифференцируемые функции от x. На основании формулы дифференциала произведения имеем
d(uv)=udv+vdu, udv=d(uv)-vdu. Интегрируя, получим
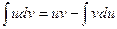
Это и есть формула интегрирования по частям. В формуле произвольной постоянной С не пишем, так как в правой части формулы остался неопределенный интеграл, содержащий произвольную постоянную. Выведенная формула показывает, что интеграл 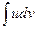 приводится к интегралу
приводится к интегралу 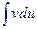 , который может оказаться более простым, чем исходный, или даже табличным.
, который может оказаться более простым, чем исходный, или даже табличным.
Эта формула чаще всего применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функции. При этом за u принимается функция, которая дифференцированием упрощается, а за dv – та часть подынтегрального выражения, содержащая dx, интеграл от которой известен или может быть найден.
Пример:
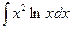 . Здесь выгодно продифференцировать lnx, т.к. тогда получится степенная функция, которая проще логарифмической, а второй множитель x2 dx интегрируем.
. Здесь выгодно продифференцировать lnx, т.к. тогда получится степенная функция, которая проще логарифмической, а второй множитель x2 dx интегрируем. 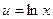 ,
, 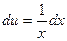 ,
, 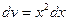 ,
, 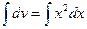 ,
, 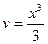
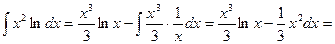
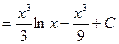
 2014-02-24
2014-02-24 408
408








