Непосредственное интегрирование
Первоначальные навыки по интегрированию связаны с так называемым непосредственным интегрированием, охватывающим применение табличных интегралов, использование свойств неопределенных интегралов и некоторых элементарных преобразований, приводящих подинтегральное выражение к виду какого-либо табличного интеграла.
Пример. Найти 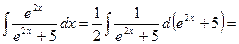
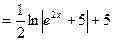
Этот способ интегрирования применяется в случаях, когда преобразования подинтегральной функции с помощью свойств неопределенного интеграла или путем разбиения ее на отдельные слагаемые не приводят к табличным формулам, но такие формулы можно получить в результате перехода к новой переменной. Этот метод интегрирования получил название метода замены переменной или метода интегрирования подстановкой.
Пусть 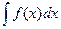 не может быть непосредственно преобразован к виду табличного. Введем новую переменную t зависимостью
не может быть непосредственно преобразован к виду табличного. Введем новую переменную t зависимостью 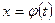 , где
, где 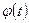 - дифференцируемая функция от t, тогда
- дифференцируемая функция от t, тогда 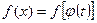 ;
;
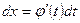
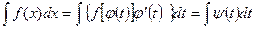
При удачном выборе замены 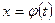 интеграл
интеграл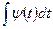 может быть переведен к одному из табличных, и тогда удается найти первообразную
может быть переведен к одному из табличных, и тогда удается найти первообразную 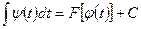 .
.
Затем выполняется обратная замена переменной t на x, первообразная функция от t преобразовывается в функцию F(x).
 2014-02-24
2014-02-24 461
461







