Достаточные условия экстремума для функции 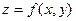 выражаются с помощью определителя:
выражаются с помощью определителя:
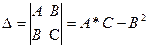 , где
, где
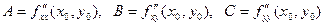 ,
,
а именно:
1) если 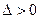 , то
, то 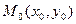 - точка экстремума:
- точка экстремума:
при A<0 (или C<0)- точка max?
при A<0 (или C>0)- точка min,
2) если 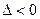 , то в точке
, то в точке 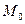 нет экстремума;
нет экстремума;
3) если 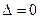 , то вопрос о наличии или отсутствии экстремума функции остается открытым.
, то вопрос о наличии или отсутствии экстремума функции остается открытым.
Пример 1. Исследовать на экстремум функцию:
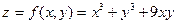 .
.
Решение. Находим частные производные первого и второго порядка:
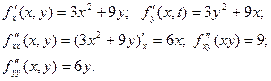
Решаем систему уравнений для определения стационарных точек:
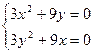 или
или 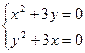 ;
;
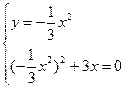 ;
; 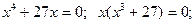
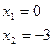 . Тогда
. Тогда 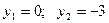 . Получаем две стационарные точки
. Получаем две стационарные точки 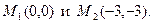 Вычислим значения частных производных второго порядка в этих точках:
Вычислим значения частных производных второго порядка в этих точках:
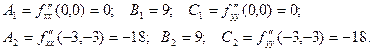
Находим определители:
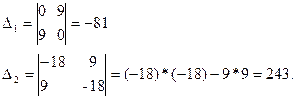
Так как 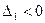 , то в точке
, то в точке 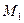 нет экстремума.
нет экстремума.
Так как 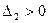 и
и 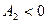 , то в точке
, то в точке 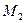 функция имеет максимум:
функция имеет максимум:
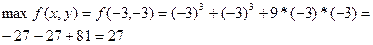 .
.
 2014-02-24
2014-02-24 867
867








