Лекция № 25-28
Список используемой литературы
1. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.1. – М.: ОНИКС. 2003. – 304 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.2. – М.: ОНИКС. 2003 – 415 с
3. Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с
4. Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.
5. Колесников, А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М.,2001, - 208 с.
6. Кремер, Н.Ш. Высшая математика для экономистов: Учебник для вузов. - М.: ЮНИТИ, 2004. – 471 с.
Тема «Дифференциальные уравнения первого порядка»
Цель: дать общие понятия дифференциальных уравнений первого порядка, привить навыкирешения линейного дифференциального уравнения методом вариации произвольной постоянной.
Ключевые слова: дифференциальное уравнение, дифференциальные уравнения первого порядка
Вопросы:
1.Общие понятия.
2.Дифференциальные уравнения первого порядка.
3.Геометрический смысл дифференциального уравнения.
4.Дифференциальные уравнения первого порядка с разделяющими переменными.
5.Однородные дифференциальные уравнения первого порядка.
6.Линейные дифференциальные уравнения первого порядка.
7.Решение линейного дифференциального уравнения методом вариации произвольной постоянной.
Уравнения связывающие между собой независимую переменную x, искомую функцию y и ее производные различных порядков по x называются дифференциальными уравнениями. Порядок старшей производной, входящей в данное дифференциальное уравнение, называется порядком этого уравнения.
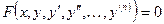 (1) – общий вид дифференциального уравнения n-го порядка.
(1) – общий вид дифференциального уравнения n-го порядка.
Например: 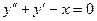 - дифференциальное уравнение II – порядка,
- дифференциальное уравнение II – порядка, 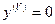 - дифференциальное уравнение V порядка.
- дифференциальное уравнение V порядка.
Дифференциальное уравнение (1) называется линейным, если левая часть его первой степени относительно функции y и ее производных 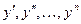 и не содержит их произведений, т.е. если это уравнение имеет вид:
и не содержит их произведений, т.е. если это уравнение имеет вид:
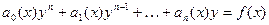 (2)
(2)
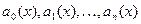 - функции от x называются коэффициентами линейного уравнения, а функция f(x) – правой частью или свободным членом его. Если f(x)=0, то (2) называется однородным (или без правой части) в противном случае это уравнение называется неоднородным (или с правой частью).
- функции от x называются коэффициентами линейного уравнения, а функция f(x) – правой частью или свободным членом его. Если f(x)=0, то (2) называется однородным (или без правой части) в противном случае это уравнение называется неоднородным (или с правой частью).
Решением дифференциального уравнения называется функция 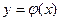 (3), которая вместе со своими производными
(3), которая вместе со своими производными 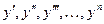 удовлетворяет уравнению (1), т.е. обращает его в тождество. Процесс отыскания решений называется интегрированием дифференциального уравнения. В общем случае для нахождения решений уравнения (1) потребуется n последовательных интегрирований, следовательно, решение общего вида будет содержать n произвольных постоянных, причем эти произвольные постоянные независимые, т.е. любую из них нельзя выразить через другие, число их равно порядку дифференциального уравнения.
удовлетворяет уравнению (1), т.е. обращает его в тождество. Процесс отыскания решений называется интегрированием дифференциального уравнения. В общем случае для нахождения решений уравнения (1) потребуется n последовательных интегрирований, следовательно, решение общего вида будет содержать n произвольных постоянных, причем эти произвольные постоянные независимые, т.е. любую из них нельзя выразить через другие, число их равно порядку дифференциального уравнения.
Общим решением дифференциального уравнения n-го порядка называется функция 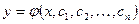 (4),
(4),
которая зависит от аргумента x и n независимых произвольных постоянных 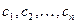 , обращающая вместе со своими производными
, обращающая вместе со своими производными 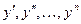 уравнение (1) в тождество.
уравнение (1) в тождество.
Общее решение, заданное в неявном виде будет:
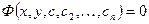 (5)
(5)
Частным решением уравнения (1) называется решение, которое получается из общего решения, если придавать постоянными 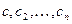 определенные числовые значения.
определенные числовые значения.
Основная задача интегрального исчисления – отыскание функции y, производная которой равна данной функции f(x), сводится к решению простейшего дифференциального уравнения.
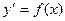 ,
, 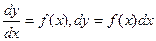 ,
, 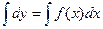
Общее решение: 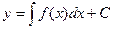
Пример. Решить уравнение 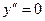
Решение. 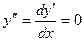 ,
,  ,
,
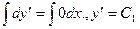 ,
, 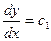 ,
, 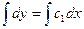 ,
,
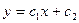 - общее решение.
- общее решение.
Решение содержит две произвольные постоянные 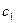 и
и 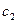 (число их равно порядку уравнения).
(число их равно порядку уравнения).
Найдем несколько частных решений.
1) 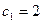 ,
, 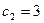 , тогда y = 2x+3
, тогда y = 2x+3
2) 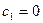 ,
, 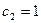 , тогда y=1 и т.д., т.е. частных решений бесконечно много.
, тогда y=1 и т.д., т.е. частных решений бесконечно много.
 2014-02-24
2014-02-24 436
436








