Дифференциальные уравнения первого порядка с разделяющими переменными.
Дифференциальным уравнением первого порядка с разделяющими переменными называются уравнения вида
 (11)
(11)
или уравнение, которое приводится к этому виду. Функции M(x), N(y), P(x), Q(y) – непрерывные. Пусть  Разделив обе части уравнения (11) на произведение, получим
Разделив обе части уравнения (11) на произведение, получим 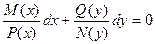 (12)
(12)
Интегрируя, найдем общий интеграл уравнения (11)
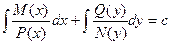 (13)
(13)
В уравнении (12) при dx стоит функция только от x, а при dy функция от y. В таком случае говорят, что переменные разделены. Соотношение (13) представляет собой общий интеграл уравнения (11), выраженный в неявной форме.
Пример. Решить дифференциальное уравнение
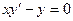
Решение. 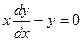 ,
, 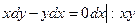
 ,
,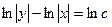 ,
, 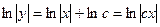
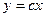 - общее решение
- общее решение
Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.
Определение. Многочлен 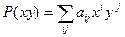 называется однородным измерения n, если все его члены имеют одно и то же измерение n, т.е. для каждого члена этого многочлена сумма показателей i+j=n
называется однородным измерения n, если все его члены имеют одно и то же измерение n, т.е. для каждого члена этого многочлена сумма показателей i+j=n
Определение. Дифференциальное уравнение
 или
или 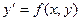 (15)
(15)
называется однородным, если функция f(x,y) однородная нулевой степени.
Уравнение (15) запишем в таком виде: 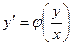 (16)
(16)
Введем новую переменную  или
или 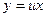 (17)
(17)
 , подставив в (16), получим:
, подставив в (16), получим:
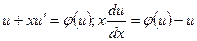
Однородное дифференциальное уравнение (15) приводится к уравнению с разделяющими переменными
 . Следовательно,
. Следовательно, 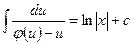 (18)
(18)
В левой части (18) найдем интеграл, вместо u подставим отношение 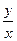 и получим искомый общий интеграл.
и получим искомый общий интеграл.
Пример. Решить дифференциальное уравнение
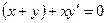
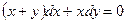 . (х+у) и х - однородные функции 1-го измерения, поэтому уравнение однородное.
. (х+у) и х - однородные функции 1-го измерения, поэтому уравнение однородное.
Полагаем  ,
, 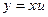 ,
, 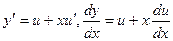
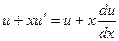 ,
, 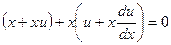
 ,
,  , делим на х,
, делим на х,
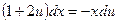 ,
,  ,
, 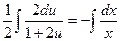
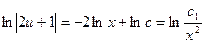 ,
, 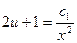 ;
; 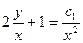 ;
; 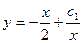 , где
, где 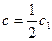
Ответ: 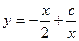
 2014-02-24
2014-02-24 773
773








