Примечания
Правила образования наименований и обозначений десятичных кратных и дольных единиц СИ
Наименования и обозначения десятичных кратных и дольных единиц СИ образуют с помощью множителей и приставок, указанных в таблице 3.
Таблица 3 – Множители и приставки
| Десятичный множитель | Приставка | Обозначение приставки | Десятичный множитель | Приставка | Обозначение приставки | ||
| между–народное | русское | Между–народное | русское | ||||
| 1024 | иотта | Y | И | 10–1 | деци | d | д |
| 1021 | зетта | Z | З | 10–2 | санти | c | с |
| 1018 | экса | E | Э | 10–3 | милли | m | м |
| 1015 | пета | P | П | 10–6 | микро | µ | мк |
| 1012 | тера | T | Т | 10–9 | нано | n | н |
| 109 | гига | G | Г | 10–12 | пико | p | п |
| 106 | мега | M | М | 10–15 | фемто | f | ф |
| 103 | кило | k | к | 10–18 | атто | a | а |
| 102 | гекто | h | г | 10–21 | зепто | z | з |
| 101 | дека | da | да | 10–24 | иокто | y | и |
Присоединение к наименованию и обозначению единицы двух или более приставок подряд не допускается. Например, вместо наименования единицы микромикрофарад следует писать пикофарад.
1. В связи с тем, что наименование основной единицы массы – килограмм содержит приставку «кило», для образования кратных и дольных единиц массы используют дольную единицу массы – грамм (0,001 kg), и приставки присоединяют к слову «грамм», например миллиграмм (mg, мг) вместо микрокилограмм (µkg, мккг).
2. Дольную единицу массы – грамм допускается применять, не присоединяя приставку.
3. Приставку или ее обозначение следует писать слитно с наименованием единицы или, соответственно, с обозначением последней.
4. Если единица образована как произведение или отношение единиц, приставку или ее обозначение присоединяют к наименованию или обозначению первой единицы, входящей в произведение или в отношение.
Правильно: килопаскаль–секунда на метр (kPa·s/m; кПа·с/м).
Неправильно: паскаль–килосекунда на метр (Pa·ks/m; Па·кс/м).
Присоединять приставку ко второму множителю произведения или к знаменателю допускается лишь в обоснованных случаях, когда такие единицы широко распространены и переход к единицам, образованным в соответствии с первой частью настоящего пункта, связан с трудностями, например: тонна–километр (t·km; т·км), вольт на сантиметр (V/cm; В/см), ампер на квадратный миллиметр (A/mm2; А/мм2).
5. Наименования кратных и дольных единиц исходной единицы, возведенной в степень, образуют, присоединяя приставку к наименованию исходной единицы. Например, для образования наименования кратной или дольной единицы площади – квадратного метра, представляющей собой вторую степень единицы длины – метра, приставку присоединяют к наименованию этой последней единицы: квадратный километр, квадратный сантиметр и т. д.
6. Обозначения кратных и дольных единиц исходной единицы, возведенной в степень, образуют добавлением соответствующего показателя степени к обозначению кратной или дольной единицы исходной единицы, причем показатель означает возведение в степень кратной или дольной единицы (вместе с приставкой).
Пример: 5·km2 = 5·(103·m)2 = 5·106 m2.
ГОСТ 8.417–2002 допускает к применению внесистемные единицы, указанные в таблице 4, без ограничения срока наравне с единицами СИ.
Таблица 4 – Внесистемные единицы, допустимые к применению наравне с единицами СИ
| Наименование физической величины | Единица измерения | ||||
| Наименование | Обозначение | Соотношение с единицей СИ | Область применения | ||
| между–народ–ное | русское | ||||
| Время | минута час сутки | min h d | мин ч сут | 60 s 3600 s 86400 s | Все области |
| Площадь | гектар | ha | га | 1·104 m2 | Сельское и лесное хозяйство |
Продолжение таблицы 4.
| Масса | тонна | t | Т | 1·103 kg | Все области |
| атомная единица массы | u | а.е.м. | 1,6605402·10–27 kg (приблизительно) | Атомная физика | |
| карат | – | кар | 2·10–4 kg (точно) | Добыча и производство драгоценных камней и жемчуга | |
| Плоский угол | градус минута секунда | …° …' …'' | …° …' …'' | (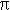 /180) rad = = 1,745329…·10–2 rad ( /180) rad = = 1,745329…·10–2 rad (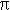 /10800) rad = = 2,908882…·10–4 rad ( /10800) rad = = 2,908882…·10–4 rad (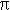 /648000) rad = = 4,848137…·10–6 rad /648000) rad = = 4,848137…·10–6 rad | Все области |
| град (гон) | gon | град | (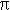 /200) rad = = 1,57080…·10–2 rad /200) rad = = 1,57080…·10–2 rad | Геодезия | |
| Объем, вместимость | литр | l | л | 1·10–3 m3 | Все области |
| Длина | астрономическая единица световой год парсек | ua ly pc | а.е. св.год пк | 1,49598·1011 m (приблизительно) 9,4605·1015 m (приблизительно) 3,0857·1016 m (приблизительно) | Астрономия |
| Длина | морская миля | n mile | миля | 1852 m (точно) | Морская навигация |
| Давление | бар | bar | бар | 1·105 kg | Физика |
| Оптическая сила | диоптрия | – | дптр | 1 m–1 | Оптика |
| Энергия | электрон–вольт | eV | эВ | 1,60218·10–19 J (приблизительно) | Физика |
| киловатт–час | kW·h | кВт·ч | 3,6·106 J | Для счетчиков электрической энергии | |
| Полная мощность | вольт–ампер | V·A | В·А | Электротехника | |
| Реактивная мощность | вар | var | вар | Электротехника | |
| Электрический заряд, количество электричества | ампер–час | A·h | А·ч | 3,6·103 C | Электротехника |
| Линейная плотность | текс | tex | текс | 1·10–6 kg/m (точно) | Текстильная промышленность |
| Скорость | узел | kn | уз | 0,514(4) m/s | Морская навигация |
| Частота вращения | оборот в секунду оборот в минуту | r/s r/min | об/с об/мин | 1 s–1 1/60 s–1 = 0,016(6) s–1 | Электротех–ника |
Измерение является важнейшим понятием в метрологии. Это организованное действие человека, выполняемое для количественного познания свойств физического объекта с помощью определения опытным путем значения какой–либо физической величины.
Существует несколько видов измерений. При их классификации обычно исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов.
По характеру зависимости измеряемой величины от времени измерения разделяются на:
― статические, при которых измеряемая величина остается постоянной во времени;
― динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени.
Статическими измерениями являются, например, измерения размеров тела, постоянного давления, динамическими – измерения пульсирующих давлений, вибраций.
По числу измерений они делятся на однократные и многократные. Однократным называют измерение, выполненное один раз. Многократным называют измерение физической величины одного размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений. Многократное измерение выполняют в случае, когда случайная составляющая погрешности однократного измерения может превысить требуемые по условиям задачи значение. Выполнив ряд последовательных отдельных измерений, получают одно многократное измерение, погрешность которого может быть уменьшена методами математической статистики.
По способу получения результатов измерений их разделяют на:
― прямые;
― косвенные;
― совокупные;
― совместные.
Прямые – это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой Q = X, где Q – искомое значение измеряемой величины, а X – значение, непосредственно получаемое из опытных данных.
При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении, а также при контроле технологических процессов (измерение давления, температуры).
Косвенные – это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле Q = F(x1,x2,…,xn), где Q – искомое значение косвенно измеряемой величины; F – функциональная зависимость, которая заранее известна, x1,x2,…,xn – значения величин, измеренных прямым способом.
Совокупные – это производимые одновременно измерения нескольких одноименных величин, при которых искомую определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.
Совместные – это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними.
По условиям, определяющим точность результата, измерения делятся на три класса:
― измерения максимально возможной точности, достижимой при существующем уровне техники. К этому же классу относятся и некоторые специальные измерения, требующие высокой точности;
― контрольно–поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения;
― технические измерения, в которых погрешность результата определяется характеристиками средств измерений.
По способу выражения результатов измерений различают абсолютные и относительные измерения.
Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.
Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.
Существуют и другие классификации измерений, например, по связи с объектом (контактные и бесконтактные), по условиям измерений (равноточные и неравноточные).
Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность.
Принцип измерений – физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.
В настоящее время все измерения в соответствии с физическими законами, используемыми при их проведении, сгруппированы в 13 видов измерений. Им в соответствии с классификацией были присвоены двухразрядные коды видов измерений: геометрические (27), механические (28), расхода, вместимости, уровня (29), давления и вакуума (30), физико–химические (31), температурные и теплофизические (32), времени и частоты (33), электрические и магнитные (34), радиоэлектронные (35), виброакустические (36), оптические (37), параметров ионизирующих излучений (38), биомедицинские (39).
Метод измерений – совокупность приемов использования принципов и средств измерений.
Метод измерений – прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений. Как правило, метод измерений обусловлен устройством средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства. Примерами распространенных методов измерений являются следующие методы:
― метод непосредственной оценки – метод, при котором значение величины определяют непосредственно по показывающему средству измерений. Например, взвешивание на циферблатных весах или измерение давления пружинным манометром;
― дифференциальный метод – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Этот метод может дать очень точные результаты. Так, если разность составляет 0,1 % измеряемой величины и оценивается прибором с точностью до 1 %, то точность измерения искомой величины составит уже 0,001 %. Например, при сравнении одинаковых линейных мер, где разность между ними определяется окулярным микрометром, позволяющим ее оценить до десятых долей микрона;
― нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Мера – средство измерений, предназначенное для воспроизведения и хранения физической величины. Например, измерение массы на равноплечных весах при помощи гирь. Принадлежит к числу очень точных методов.
― метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают величиной, воспроизводимой мерой. Например, измерение напряжения постоянного тока на компенсаторе сравнением с известной ЭДС нормального элемента. Результат измерения при этом методе либо вычисляют как сумму значения используемой для сравнения меры и показания измерительного прибора, либо принимают равным значению меры. Существуют различные модификации этого метода: метод измерения замещением (измеряемую величину замещают мерой с известным значением величины, например, при взвешивании поочередным помещением массы и гирь на одну и ту же чашку весов) и метод измерений дополнением (значение измеряемой меры дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению).
Качество измерений характеризуется точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также размером погрешности.
Погрешность измерений – разность между полученным при измерении и истинным значениями измеряемой величины. Погрешность вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а также недостаточным опытом наблюдателя или особенностями его органов чувств.
Точность измерений – это характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины. Количественно точность можно выразить величиной, обратной модулю относительной погрешности.
Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в частности, от того, насколько действительный размер единицы, в которой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.
Важнейшей характеристикой качества измерений является их достоверность. Она характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации.
Сходимость (повторяемость) – это качество измерений, отражающее близость друг к другу результатов измерений одного и того же параметра, выполненных повторно одними и теми же средствами измерений, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.
Воспроизводимость – это качество измерений, отражающее близость друг к другу результатов измерений одного и того же параметра, выполняемых в различных условиях (в различное время, различными средствами и т.д.).
 2014-02-09
2014-02-09 1285
1285
