При расчете на устойчивость рабочая нагрузка назначается как n -я доля критической, где под n понимается запас устойчивости.
Задача Эйлера.
Рассмотрим равновесие стержня, сжатого центральными силами
При малых прогибах EI y
 = M. I = Imin т.к. изгиб происходит в плоскости минимальной жесткости.
= M. I = Imin т.к. изгиб происходит в плоскости минимальной жесткости.

Изгибающий момент М = F y считается положительным, если увеличивает кривизну.
На рисунке М уменьшает кривизну т.к. при положительном у упругая линия имеет выпуклость вверх следовательно кривизна отрицательна.
Момент силы F еще сильнее искривляет упругую линию т.е. уменьшает ее кривизну. EI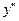 = -F y.
= -F y.
Обозначим k2 = 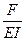 , тогда
, тогда 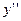 +k2y=0.
+k2y=0.
Отсюда у= С1 sinkz+С2 coskz. При z = 0, y = 0 отсюда С2 = 0.
При z=l y=0 отсюда C1 sinkl = 0. Это уравнение имеет два возможных решения: 1) С1 = 0. Тогда при С1= С2 = 0 у=0 этот случай не интересует.
2) kl=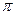 n, n- целое число. В этом случае k2=
n, n- целое число. В этом случае k2=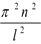 =
=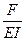 ; или F=
; или F=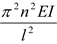 .
.
Это означает, что для того, чтобы стержень сохранял криволинейную форму, необходимо, чтобы F принимала определенное значение. Наименьшая сила будет при n=1.
Fкр . = 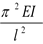 – критическая или Эйлерова сила.
– критическая или Эйлерова сила.
При n=1, kl=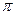 и решение будет иметь вид: y=C1 sin
и решение будет иметь вид: y=C1 sin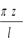 - стержень изгибается по полуволне синусоиды с максимальным прогибом С1.
- стержень изгибается по полуволне синусоиды с максимальным прогибом С1.
При любом целочисленном n y=C1 sin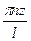 - упругая линия имеет п полуволн.
- упругая линия имеет п полуволн.
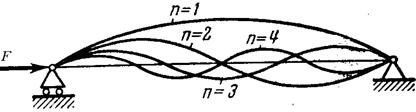
Величина С1 остается неопределенной т.к. было использовано приближенное уравнение при малых прогибах у. При силе F большей критической, перемещения растут быстро и пренебречь величиной (у’) 2 в знаменателе дифференциального уравнения изогнутой оси нельзя.
Зависимость критической силы от условий закрепления стержня.
Используя особенности упругой линии, полученное решение можно распространить и на другие случаи закрепления стержня. Так, если стержень на одном конце жестко защемлен, а на другом свободен, то упругую линию стержня путем зеркального отображения легко привести к упругой линии шарнирно закрепленного стержня.
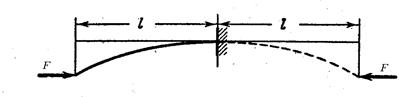
В данном случае критическая сила будет равна Fкр. шарнирно закрепленного стержня, имеющего длину 2 l, т.е.
Fкр. = 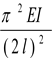 .
.
Для стержня, имеющего посредине опору, как шарнирно опертый стержень длиной 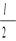 .
.
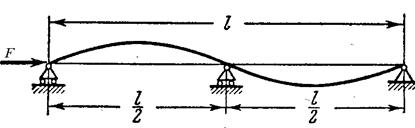
Fкр .= 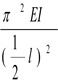 .
.
Обобщая можно записать общее выражение:
Fкр. = 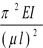 , где
, где
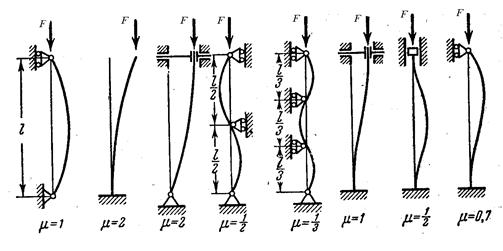
μ-коэффициент приведения длины, число показывающее, во сколько раз следует увеличить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной l в рассматриваемых условиях закрепления.
Значения μ для различных случаев закрепления концов стержня приводится в учебниках или в пособии по курсу.
Устойчивость стержня при наличии пластических деформаций.
Расчет по коэффициентам уменьшения допускаемых напряжений.
Все полученные выше формулы предполагают наличие только упругих деформаций, т.е. для сравнительно длинных и тонких стержней.
Для более коротких и жестких стержней Fкр. будет большей и возможно возникновение пластических деформаций до потери устойчивости.
Определим критическое напряжение из расчета действия критической силы:
σкр.=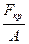 =
=
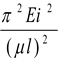 , где i2=
, где i2=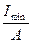 - радиус инерции сечения.
- радиус инерции сечения.
Обозначим λ = 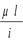 - гибкость стержня, тогда σкр.=
- гибкость стержня, тогда σкр.= 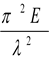 .
.
Если σкр. = σТС формула Эйлера становится неприменимой. В этом случае предельная гибкость определяется при σ = σпц.
λпред=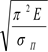 .
.
При λ<λпред-формула Эйлера неприменима и в стержне возникают пластические деформации.
При λ>λпред формула Эйлера применима и стержень работает в упругой стадии.
Для расчета на устойчивость и определения σкрит за пределом упругости строится график зависимости σкрит.- λ для всех реально встречающихся значений гибкости λ, начиная от нуля.
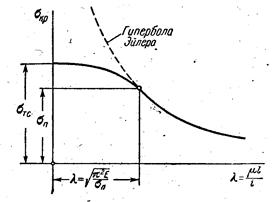 Обозначим φ =
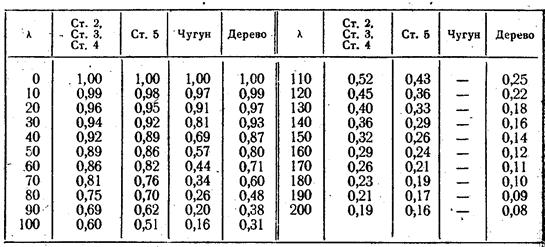
Обозначим φ = 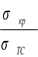 , тогда σкр.=φσТС. Соответственно допускаемое напряжение [σ]кр = φ[σ]C, следовательно, расчет стержня на устойчивость можно заменить обычным расчетом по пределу текучести, но со сниженным [σ]. Вместо [σ]c, берется φ[σ]c. Величина φ называется коэффициентом снижения допускаемого напряжения. С увеличением гибкости λ, φ снижается. Коэффициент φ для наиболее часто встречающихся материалов вычисляется заранее и приводится в таблицах в зависимости от гибкости λ.
, тогда σкр.=φσТС. Соответственно допускаемое напряжение [σ]кр = φ[σ]C, следовательно, расчет стержня на устойчивость можно заменить обычным расчетом по пределу текучести, но со сниженным [σ]. Вместо [σ]c, берется φ[σ]c. Величина φ называется коэффициентом снижения допускаемого напряжения. С увеличением гибкости λ, φ снижается. Коэффициент φ для наиболее часто встречающихся материалов вычисляется заранее и приводится в таблицах в зависимости от гибкости λ.
Пример: Определить Fдоп для сжатого шарнирно закрепленного стержня l=2 м. Поперечное сечение -двутавр №30, imin=2,95см, A=49,9см2, [σ]=200МПа.
Решение: Определяем гибкость λ=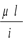 =
=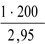 = 67,8. По табл. при λ=67,8;φ=0,82. Тогда
= 67,8. По табл. при λ=67,8;φ=0,82. Тогда 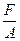 = [σ]cφ и F = [σ]cφA = 200 106 0,82 49,9 10-4 = 82 104Н = 820 КН
= [σ]cφ и F = [σ]cφA = 200 106 0,82 49,9 10-4 = 82 104Н = 820 КН
Тема 12. Прочность при напряжениях циклически изменяющихся во времени.
Лекция 10. Основные понятия.
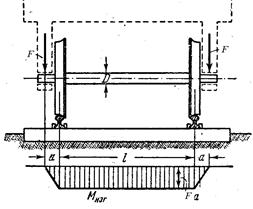
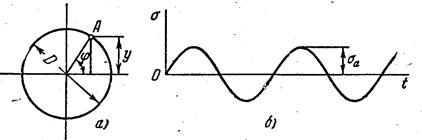
При вращении оси вагона, в точках на поверхности в произвольном сечении напряжения будут менять знак и величину.
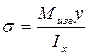
Расстояние у от точки А до нейтральной оси меняется во времени 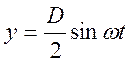
Где ω –угловая скорость вращения колеса. Следовательно: 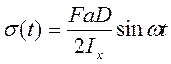
Т.е. нормальное напряжение в сечении оси меняется по синусоиде с амплитудой
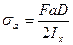
 2014-02-24
2014-02-24 1066
1066
