Опр Носителем КЗФ 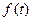 на оси
на оси 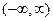 называется замыкание множества точек, в которых
называется замыкание множества точек, в которых 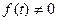 . Обозначение
. Обозначение 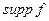 .
.
Пр. Носитель функции Хевисайда 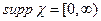 .
.
Опр Пространствомосновных (финитных) функций называется пространство 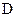 бесконечно дифференцируемых функций, на
бесконечно дифференцируемых функций, на 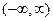 , которые имеют компактный (то есть ограниченный) носитель.
, которые имеют компактный (то есть ограниченный) носитель.
Пр Функция шапочка 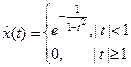 - бесконечно дифференцируема на
- бесконечно дифференцируема на 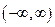 и финитная с носителем
и финитная с носителем 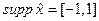 .
.
Опр Последовательность финитных функций 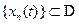 называется сходящейся к нулю, если
называется сходящейся к нулю, если 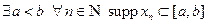 , и
, и 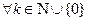 последовательности
последовательности 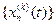 равномерно стремятся к нулю на
равномерно стремятся к нулю на 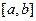 .
.
Обозначение  .
.
Опр Линейный функционал 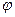 на пространстве
на пространстве 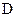 называется непрерывным функционалом (обобщенной функцией), если
называется непрерывным функционалом (обобщенной функцией), если 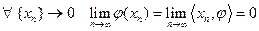 .
.
Обозначение 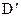 - пространство обобщенных функций.
- пространство обобщенных функций.
Пр 1 Каждый оригинал 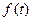 определяет обобщенную функцию на пространстве
определяет обобщенную функцию на пространстве  по правилу
по правилу 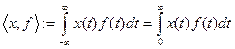 .
.
Пр 2 Каждая функция 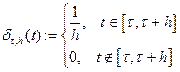 определяет обобщенную функцию по правилу
определяет обобщенную функцию по правилу 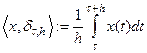 .
.
Опр Обобщенная функция 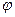 называется регулярной, если она порождена локально суммируемой (то есть суммируемой на каждом отрезке из
называется регулярной, если она порождена локально суммируемой (то есть суммируемой на каждом отрезке из 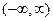 ) функцией
) функцией 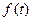 по правилу
по правилу 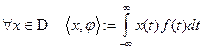 .
.
Опр 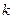 - ой производной обобщенной функции
- ой производной обобщенной функции  называется функционал
называется функционал 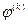 на пространстве
на пространстве 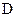 , определяемый по правилу
, определяемый по правилу 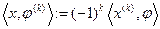 .
.
ЗАМЕЧАНИЕ 1) Производная обобщенной функции будет функцией обобщенной.
2) Если регулярная обобщенная функция 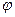 порождена
порождена 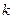 раз непрерывно дифференцируемой функцией
раз непрерывно дифференцируемой функцией 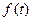 , то
, то 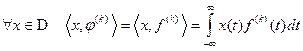 .
.
Опр Линейный функционал 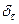 на
на 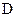 , определяемый по правилу
, определяемый по правилу 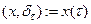 ,
,
называется  - функцией (единичным импульсом, функцией Дирака).
- функцией (единичным импульсом, функцией Дирака).
ТЕОРЕМА 10.13 (свойства  -функции) 1)
-функции) 1) 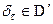 .
.
2) 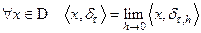 , то есть
, то есть 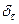 является слабым пределом последовательности регулярных обобщенных функций, порожденных функциями
является слабым пределом последовательности регулярных обобщенных функций, порожденных функциями 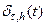 .
.
3)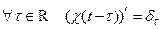 . 4)
. 4)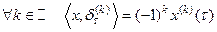 .
.
ЗАМЕЧАНИЕ 1 (физический смысл  -функции) Плотностью материальной точки с координатой
-функции) Плотностью материальной точки с координатой 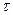 и массой
и массой 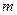 равна обобщенной функции
равна обобщенной функции 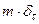 .
.
◄ По физическому смыслу точка является пределом последовательности интервалов массы 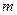 с однородной плотностью, которые стягиваются к этой точке. Функция плотности такого интервала равна
с однородной плотностью, которые стягиваются к этой точке. Функция плотности такого интервала равна 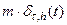 , так как
, так как 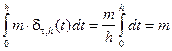 . Рассматривая ее как регулярную обобщенную функцию, имеем
. Рассматривая ее как регулярную обобщенную функцию, имеем 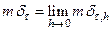 . ►
. ►
СЛЕДСТВИЕ Плотность системы материальных точек на оси с координатами 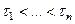 и массами соответственно
и массами соответственно 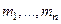 равна
равна 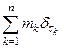 .
.
ЗАМЕЧАНИЕ 2 (физический смысл  -функции) Ударным импульсом силы величины
-функции) Ударным импульсом силы величины 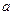 , приложенным к материальной точке с координатой
, приложенным к материальной точке с координатой 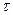 называется обобщенная функция
называется обобщенная функция 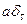 .
.
____
Опр Обозначим 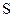 пространство бесконечно дифференцируемых на оси
пространство бесконечно дифференцируемых на оси 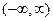 функций, у которых каждая производная убывает на бесконечности быстрее любой степени
функций, у которых каждая производная убывает на бесконечности быстрее любой степени 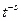 :
: 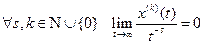 .
.
Пр 1 Функция 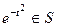 .
.
Пр 2 «Шапочка» 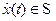 , так как имеет компактный носитель
, так как имеет компактный носитель 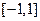 и бесконечно дифференцируема на
и бесконечно дифференцируема на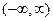 .
.
Опр Последовательность функций 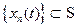 называется сходящейся к нулю,если
называется сходящейся к нулю,если 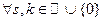 последовательности
последовательности 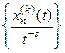 равномерно на оси
равномерно на оси 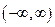 стремится к нулю, когда
стремится к нулю, когда 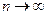 .
.
Опр Линейный функционал 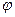 на пространстве
на пространстве 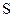 называется непрерывным (обобщен ной функцией медленного роста), если
называется непрерывным (обобщен ной функцией медленного роста), если 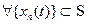 , сходящейся к нулю,
, сходящейся к нулю, 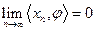 .
.
Обозначение 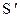 - пространство обобщенных функций медленного роста.
- пространство обобщенных функций медленного роста.
ЗАМЕЧАНИЕ 1 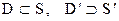 .
.
ЗАМЕЧАНИЕ 2 Запас обобщенных функций из 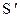 достаточно богат. Например, измеримые функции медленного роста, то есть функции, для которых при некотором
достаточно богат. Например, измеримые функции медленного роста, то есть функции, для которых при некотором 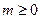 сходится интеграл
сходится интеграл 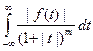 , определяют регулярные обобщенные функции из
, определяют регулярные обобщенные функции из 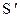 . Таковы, например, функции
. Таковы, например, функции 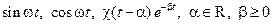 .
.
Опр Носителем обобщенной функции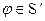 называется такое наименьшее замкнутое множество
называется такое наименьшее замкнутое множество 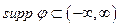 , что
, что 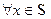 выполняется условие: если
выполняется условие: если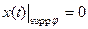 , то
, то 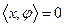 .
.
Пр 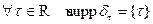 .
.
Опр Произведением бесконечно дифференцируемой на оси функции 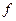 на обобщенную
на обобщенную
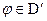 называется обобщенная функция
называется обобщенная функция 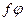 , определяемая по правилу
, определяемая по правилу 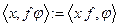
Опр Обозначим 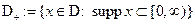 . Обобщенная функция
. Обобщенная функция 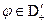 ,называется
,называется
обобщенным оригиналом,если 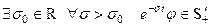 .
.
Пр 1 Обычный оригинал 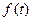 порождает регулярную обобщенную функцию над
порождает регулярную обобщенную функцию над 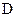 по правилу
по правилу 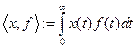 , которая является обобщенным оригиналом с
, которая является обобщенным оригиналом с 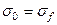 .
. 
Пр 2 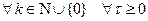 обобщенные функции
обобщенные функции 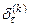 являются обобщенными оригина- лами. Действительно, пусть
являются обобщенными оригина- лами. Действительно, пусть 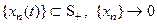 . Тогда
. Тогда 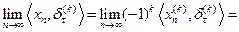
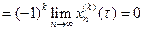 , откуда
, откуда 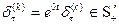 , то есть
, то есть 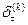 обобщенный оригинал.
обобщенный оригинал.
Опр Изображением обобщенного оригинала 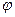 называется функция комплексного переменного в полуплоскости
называется функция комплексного переменного в полуплоскости 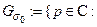
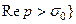 , определяемая по правилу
, определяемая по правилу
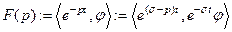 , где
, где 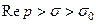 .
.
Пр 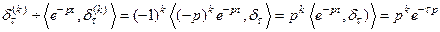 .
.
Опр Правило, сопоставляющее обобщенному оригиналу его изображение, называется обобщенным преобразованием Лапласа.
ЗАМЕЧАНИЕ (свойства) 1) Изображение 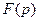 является аналитической в полуплоско сти
является аналитической в полуплоско сти 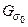 функцией. 2) (теорема Шварца) Аналитическая в какой-либо полуплоскости
функцией. 2) (теорема Шварца) Аналитическая в какой-либо полуплоскости 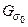 функция
функция 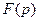 является изображением обобщенного оригинала тогда и только тог да, когда
является изображением обобщенного оригинала тогда и только тог да, когда 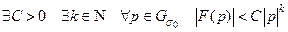 . 3) Множества обобщенных оригиналов
. 3) Множества обобщенных оригиналов 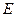 и изображений обобщенных оригиналов
и изображений обобщенных оригиналов 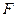 являются векторными пространствами и обобщенное преобразование Лапласа является изоморфизмом
являются векторными пространствами и обобщенное преобразование Лапласа является изоморфизмом 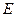 на
на 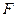 .
.
Пр Материальная точка массы 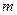 совершает прямолинейные горизонтальные колебания без трения под действием силы
совершает прямолинейные горизонтальные колебания без трения под действием силы 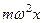 , пропорциональной отклонению
, пропорциональной отклонению 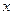 . В моменты времени
. В моменты времени 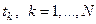 , на нее действуют импульсы силы
, на нее действуют импульсы силы 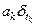 соответственно. Определить закон движения точки. В начальный момент времени точка находится в положении
соответственно. Определить закон движения точки. В начальный момент времени точка находится в положении 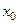 и имеет скорость
и имеет скорость 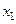 .
.
◄ В соответствии с условием искомый закон 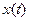 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 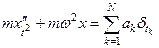 с начальным условием
с начальным условием 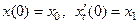 .
.
Решение однородного 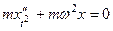 с этим условием имеет вид
с этим условием имеет вид 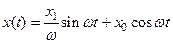 .
.
Для нахождения частного решения исходного уравнения с нулевыми начальными условиями используем обобщенное преобразование Лапласа. Учитывая 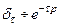 , имеем
, имеем
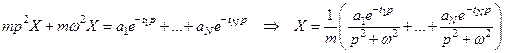 .
.
Тогда обратное преобразование дает частное решение
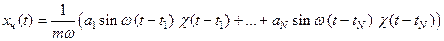 .
.
Поэтому искомое колебание материальной точки осуществляется по закону
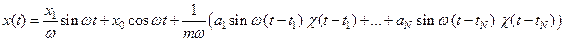 .
.
Дифференцированием нетрудно убедиться, что в момент времени 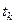 скорость материальной
скорость материальной
точки скачком изменяется на величину 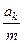 .►
.►
 2014-02-24
2014-02-24 1516
1516
