Опр Графом называется пара 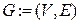 , состоящая из конечного множества
, состоящая из конечного множества 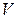 точек (вершины (vertex) графа) и подмноже ства
точек (вершины (vertex) графа) и подмноже ства 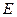 упорядоченных пар вершин (дуги графа) или неупорядочен ных пар вершин (ребра (edge) графа).
упорядоченных пар вершин (дуги графа) или неупорядочен ных пар вершин (ребра (edge) графа).
◄ В соответствии с условием искомый закон 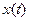 удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению 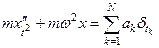 с начальным условием
с начальным условием 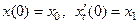 .
.
Решение однородного уравнения 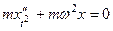 с этим условием имеет вид
с этим условием имеет вид 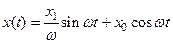 .
.
Для нахождения частного решения исходного уравнения с нулевыми начальными условиями используем обобщенное преобразование Лапласа. Учитывая 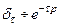 , имеем
, имеем
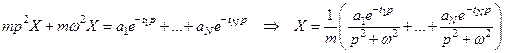 .
.
Тогда обратное преобразование дает частное решение
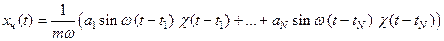 .
.
Поэтому искомое колебание материальной точки осуществляется по закону
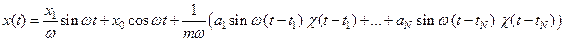 .
.
Дифференцированием нетрудно убедиться, что в момент времени 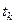 скорость материальной точки скачком изменяется на величину
скорость материальной точки скачком изменяется на величину 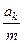 .►
.►
 2014-02-24
2014-02-24 524
524








