Опр Пусть функция 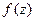 аналитическая на кривой
аналитическая на кривой 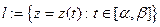 и
и 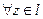 . Это
. Это 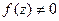 обеспечивает непрерывность аргумента функции
обеспечивает непрерывность аргумента функции 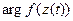 на кривой. Произведем разбиение
на кривой. Произведем разбиение 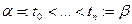 отрезка
отрезка 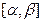 , и по функции
, и по функции 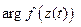 и разбиению образуем интегральную сумму
и разбиению образуем интегральную сумму 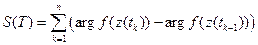 . Можно доказать, что существует конечный предел
. Можно доказать, что существует конечный предел 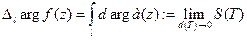 ,. Его называют изменением аргумента функции
,. Его называют изменением аргумента функции 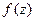 вдоль кривой
вдоль кривой 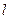 .
.
ТЕРЕМА 10.7 1) 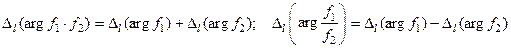 .
.
2) Пусть кривая 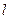 разбита на два куска:
разбита на два куска: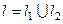 . Тогда
. Тогда 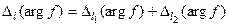 .
.
3) 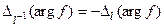 . 4) (принцип аргумента) Пусть функция
. 4) (принцип аргумента) Пусть функция 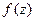 непрерывна на
непрерывна на
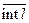 и аналитическая внутри замкнутой спрямляемой жордановой кривой
и аналитическая внутри замкнутой спрямляемой жордановой кривой 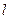 за
за
исключением конечного числа полюсов. Пусть 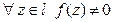 . Тогда, если
. Тогда, если 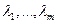 - нули
- нули 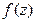 в
в 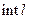 с кратностями соответственно
с кратностями соответственно 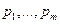 ,
, 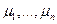 - ее полюсы в
- ее полюсы в 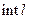 порядков
порядков 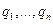 , то
, то 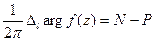 , где
, где 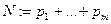 ,
, 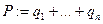 .
.
ЗАМЕЧАНИЕ В Matlab многочлен 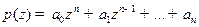 задается массивом коэффициентов в виде
задается массивом коэффициентов в виде 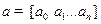 . Операция нахождения нулей этого многочлена задается функцией
. Операция нахождения нулей этого многочлена задается функцией  roots (a).
roots (a).
_____
Опр Пусть функция 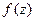 аналитическая на кривой
аналитическая на кривой 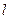 . Годографом функции
. Годографом функции 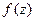 относительно этой кривой называется ее образ
относительно этой кривой называется ее образ 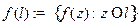 .
.
ЗАМЕЧАНИЕ (геометрический смысл изменения аргумента функции вдоль кривой) Изменения аргумента функции 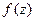 вдоль кривой, деленный на
вдоль кривой, деленный на 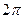 , совпадает с числом оборотов точки
, совпадает с числом оборотов точки 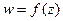 вокруг начала координат при ее движении по годографу
вокруг начала координат при ее движении по годографу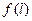 ).
).
Пр 1 Найдем число корней алгебраического уравнения 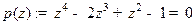 в правой полуплоскости.
в правой полуплоскости.
1) На мнимой оси
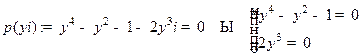 . Так как последняя система не имеет решений, то
. Так как последняя система не имеет решений, то 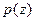 не имеет нулей на мнимой оси.
не имеет нулей на мнимой оси.
2) Все нули из правой полуплоскости содержатся внутри полукруга с границей 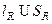 и с достаточно большим радиусом
и с достаточно большим радиусом 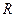 . По предыдущей теореме искомое число нулей равно
. По предыдущей теореме искомое число нулей равно 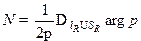 . Поэтому
. Поэтому 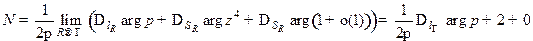 .
.
3) Найдем число оборотов 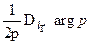 годографа
годографа 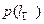 вокруг начала координат, для чего понадобится его изображение. Из параметрического задания
вокруг начала координат, для чего понадобится его изображение. Из параметрического задания 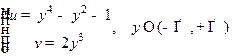 следует однозначность функции
следует однозначность функции 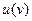 на
на 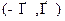 и симметричность графика относительно оси
и симметричность графика относительно оси 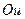 .
.
Имеем одну точку пересечения 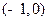 с осью
с осью 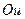 и две точки
и две точки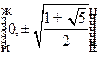 - с осью
- с осью 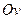
При больших значениях параметра точки графика находятся в четвертой и первой четвертях. Поэтому график схематично имеет вид 
Учитывая, что 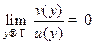 , получаем
, получаем 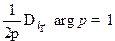 . Отсюда
. Отсюда 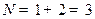 .
.
Пр 2 Найдем угол, на который годограф функции 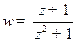 относительно мнимой оси охватывает точку
относительно мнимой оси охватывает точку 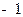 . Имеем
. Имеем 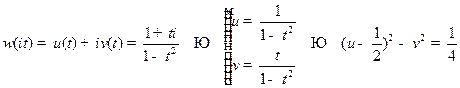 - гипербола с центром в точке
- гипербола с центром в точке 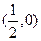 и равными
и равными 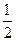 полуосями. Так как функция имеет полюсы в точках
полуосями. Так как функция имеет полюсы в точках 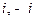 мнимой оси, то гипербола разбивается на три куска: левая верхняя полуветвь
мнимой оси, то гипербола разбивается на три куска: левая верхняя полуветвь 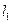 , правая ветвь
, правая ветвь 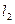 и левая нижняя полуветвь
и левая нижняя полуветвь 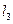 соответственно при
соответственно при 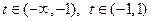 ,
, 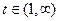 . Так как
. Так как 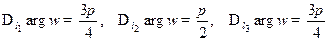 , то
, то
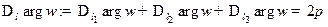 .
.
ЗАМЕЧАНИЕ Рациональная функция 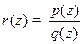 задается в Matlab с помощью функции tf(p,q). Годограф рациональной функции относительно мнимой оси строится с помощью nyquist.
задается в Matlab с помощью функции tf(p,q). Годограф рациональной функции относительно мнимой оси строится с помощью nyquist.
Пр Следующая последовательность команд позволяет построить годограф из примера 1. >> num=[1 -2 1 0 -1]; den=[1]; sys=tf(num,den); nyquist(sys)
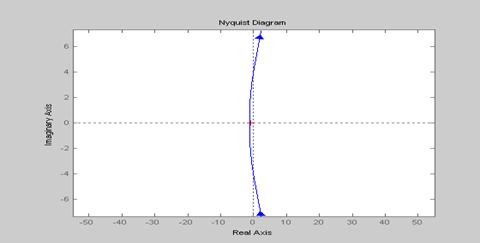
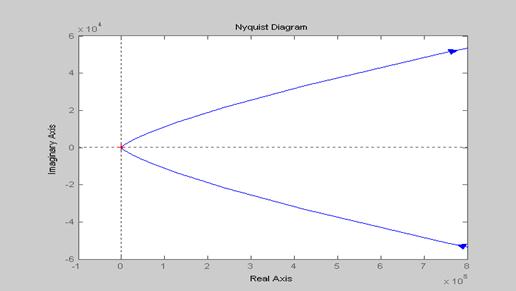
Здесь один и тот же годограф изображен в разных масштабах
_____
Определение Пусть коэффициенты многочлена зависят от 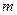 параметров
параметров 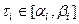 . Так как каждой допустимой
. Так как каждой допустимой 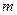 -ке
-ке 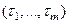 сопоставляется
сопоставляется 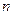 корней алгебраического уравнения
корней алгебраического уравнения 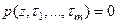 , то имеем неявное отображение из множества
, то имеем неявное отображение из множества 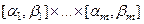 в пространство
в пространство 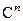 . Известно, что если коэффициенты многочлена непрерывно зависят от параметров, то при непрерывном изменении точки
. Известно, что если коэффициенты многочлена непрерывно зависят от параметров, то при непрерывном изменении точки 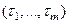 соответствующая
соответствующая 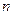 -ка корней непрерывно изменяется. Тем самым это отображение непрерывно и порождается непрерывными координатными функциями
-ка корней непрерывно изменяется. Тем самым это отображение непрерывно и порождается непрерывными координатными функциями 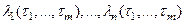 . Задаваемое ими
. Задаваемое ими 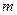 -мерное многообразие в
-мерное многообразие в 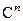 называется корневым годографом многочлена.
называется корневым годографом многочлена.
Рассмотрим специальный случай при 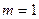 в той форме. которая имеет многочисленные применения в теории управления при изучении устойчивости и синтезе систем управления.
в той форме. которая имеет многочисленные применения в теории управления при изучении устойчивости и синтезе систем управления.
Определение Пусть 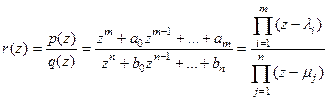 - задаваемая несократимой дробью рациональная функция степени
- задаваемая несократимой дробью рациональная функция степени 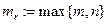 и относительной степени
и относительной степени 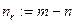 . Рассмотрим уравнение
. Рассмотрим уравнение
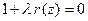 (1)
(1)
с параметром  . Оно порождает алгебраическое уравнение
. Оно порождает алгебраическое уравнение 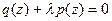 степени
степени 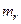 . При непрерывном изменении
. При непрерывном изменении 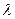 от
от 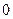 до
до 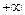 его корни в количестве
его корни в количестве 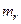 штук непрерывно изменяются, двигаясь по кривым (траекториям) в комплексной плоскости. Совокупность этих траекторий называется корневым годографом уравнения (1).
штук непрерывно изменяются, двигаясь по кривым (траекториям) в комплексной плоскости. Совокупность этих траекторий называется корневым годографом уравнения (1).
Пример Изобразить корневой годограф для пары многочленов 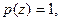
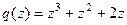 .
.
◄ Так как 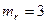 , годограф состоит из трех траекторий. Так как алгебраическое уравнение
, годограф состоит из трех траекторий. Так как алгебраическое уравнение  имеет третью степень, то траектории начинаются в точках (корнях уравнения при
имеет третью степень, то траектории начинаются в точках (корнях уравнения при 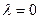 )
) 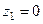 ,
, 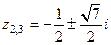 .
.
а) 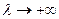 тогда и только тогда, когда все корни удаляются по своим траекториям к
тогда и только тогда, когда все корни удаляются по своим траекториям к 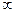 . Поэтому
. Поэтому 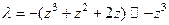 . Отсюда получаем направления
. Отсюда получаем направления 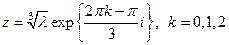 , в которых распространяются траектории с ростом
, в которых распространяются траектории с ростом 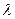 .
.
б) Так как коэффициенты уравнения вещественны, то две траектории зеркально симметричны относительно мнимой оси, а по формулы Виета для свободного члена следует, что третья траектория лежит на отрицательной части вещественной оси.
в) Если 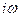 есть точка пересечения траекторий с мнимой осью, то подставляя ее в уравнение, имеем
есть точка пересечения траекторий с мнимой осью, то подставляя ее в уравнение, имеем 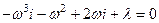 . Приравнивая нулю вещественную и мнимую части, получаем
. Приравнивая нулю вещественную и мнимую части, получаем 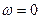 при
при 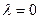 и
и  при
при 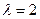 . ►
. ►
Более точную информацию о поведении корневого годографа дает
ТЕОРЕМА 10.8 (качественные свойства корневого годографа)
1) Точка 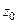 принадлежит корневому годографу тогда и только тогда, когда
принадлежит корневому годографу тогда и только тогда, когда 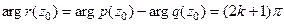 , при этом соответствующее
, при этом соответствующее 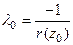 .
.
2) Пусть 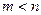 . Тогда:
. Тогда:
2а) при 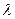 близком к
близком к 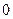
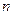 соответствующих точек годографа расположены вблизи полюсов
соответствующих точек годографа расположены вблизи полюсов 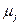 функции
функции 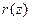 .
.
2б) при 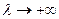
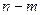 точек годографа стремятся к соответствующим
точек годографа стремятся к соответствующим 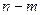 асимптотам, выходящим из точек
асимптотам, выходящим из точек 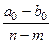 и образующих углы
и образующих углы 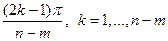 , с положительным направлением вещественной оси. Остальные
, с положительным направлением вещественной оси. Остальные 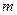 точек годографа приближаются к нулям
точек годографа приближаются к нулям 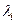 функции
функции 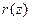 .
.
3) Если 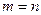 , то все траектории годографа начинаются в полюсах
, то все траектории годографа начинаются в полюсах 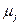 функции
функции 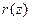 и оканчиваются в ее нулях
и оканчиваются в ее нулях 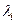 .
.
4) Пусть 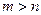 . Тогда:
. Тогда:
4а) при 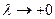
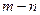 точек годографа стремятся к соответствующим
точек годографа стремятся к соответствующим 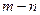 асимптотам, выходящим из точек
асимптотам, выходящим из точек 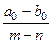 и образующих углы
и образующих углы 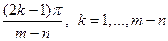 с положитель ным направлением вещественной оси. Остальные
с положитель ным направлением вещественной оси. Остальные 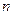 точек годографа приближаются к полюсам
точек годографа приближаются к полюсам 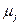 .
.
4б) при 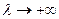
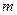 соответствующих точек годографа стремятся к соответствующим нулям
соответствующих точек годографа стремятся к соответствующим нулям 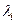 .
.
5) Для нахождения точек 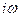 пересечения корневого годографа с мнимой осью необходи мо приравнять нулю линейный по
пересечения корневого годографа с мнимой осью необходи мо приравнять нулю линейный по 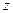 остаток от отделения многочлена
остаток от отделения многочлена 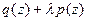 на
на 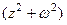 .
.
6) Точки вещественной оси, принадлежащие корневому годографу, лежит левее нечетного числа нулей и полюсов функции 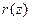 .
.
Пример (продолжение) В предыдущем примере 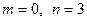 ,
, 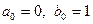 . Поэтому на основании пункта 2 теоремы имеем такое свойство годографа.
. Поэтому на основании пункта 2 теоремы имеем такое свойство годографа.
г) Асимптоты представляют собой три луча, начинающиеся в точке 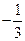 и направленные под углами
и направленные под углами 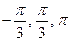 к вещественной оси.
к вещественной оси.
д) Функция 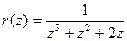 не имеет нулей, имеет один полюс в нуле и два комплексно сопряжены полюса
не имеет нулей, имеет один полюс в нуле и два комплексно сопряжены полюса 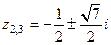 . Поэтому на основании пункта 6 теоремы точки вещественной оси, принадлежащие корневому годографу, должны лежать левее точки
. Поэтому на основании пункта 6 теоремы точки вещественной оси, принадлежащие корневому годографу, должны лежать левее точки 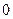 .
.
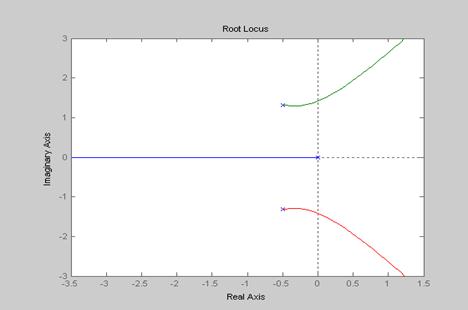
ЗАМЕЧАНИЕ В Matlab годограф строится с помощью функции rlocus.
Пр Следующая последовательность команд позволяет построить корневой годограф из последнего примера. >> p=[1]; q=[1 1 2 0]; sys=tf(p,q); rlocus(sys)
 2014-02-24
2014-02-24 2326
2326
