Опр Матрица , строками которой являются координаты вектор-циклов какого-либо циклового базиса, называется цикломатической матрицей графа

ТЕОРЕМА 12.2 (Свойства циклового базиса связного мультиграфа)

1) Если при некоторой ориентации ребер выполняется равенство

,

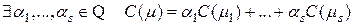то оно сохраняется при любой другой его ориентации.

2) Цикловые базисы мультиграфа имеют одно и тоже количество элементов, которое равно 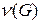, поэтому 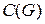имеет размер .

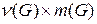3) Если связный орграф не является деревом (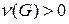), то в нем существует цикловой базис, состоящий из простых циклов.

◄ 3) (алгоритм построения)

Шаг 1. В графе 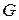строим остовное дерево 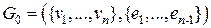, которое не содер жит 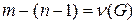– ребер 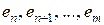. Шаг 2. Для каждого из этих ребер в 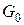по теореме 12.1.3 существует единственный простой цикл, содержащий это ребро. Полученные

циклы линейно независимы, так как ранг соответствующей цикломатической матрицы равен,

очевидно, . ►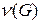

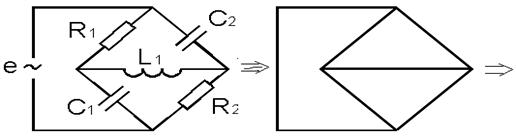
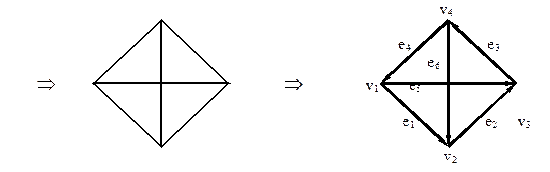
Пример По данной электрической цепи, образованной двухполюсными элементами, построим орграф и найдем цикломатическую матрицу последнего. Для этого последовательно каждую ветвь с содержащейся на ней одним элементом считаем ребром графа; ветви, не содержащие элементов, стянем в точку; на полученном графе зададим произвольную ориентация ребер. На рис. 12.11 показан порядок построения орграфа.