Ортогональные системы функций и ряды Фурье

Опр Бесконечная последовательность элементов 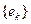евклидова пространства 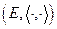называется ортогональной, если ее элементы попарно ортогональны: 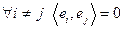, и ортонормированной, если дополнительно эти элементы нормированным: 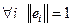, то есть .

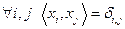Обозначение 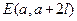- пространство функций имеющих разрывы первого рода на отрезке 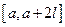и правые и левые производные в каждой точке непрерывности.

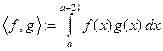- скалярное произведение в .

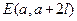Пр 1 Последовательность 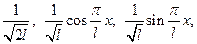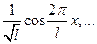ортонормирована в пространстве 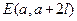, а в последовательность 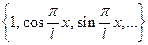ортогональна в

.

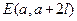◄ Например, при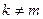

.►

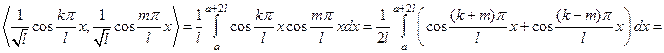
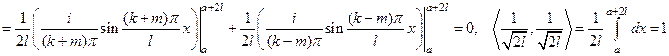Обозначение 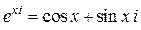- формула Эйлера (короткое обозначение комплексного числа вида 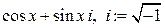. 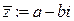- сопряженное к комплексному числу .

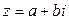Пр 2 Последовательность функций 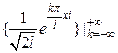, ортонормированна относительно скалярного произведения 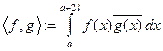на множестве комплекснозначных функций .

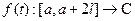Опр Пусть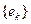-ортогональная последовательность в евклидовом пространстве 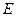. Числа 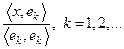, называются коэффициентами Фурье элемента 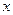по системе 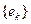. Сумма 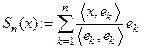называется 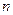-ой частичной суммой, а ряд 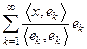- рядом Фурье элемента .

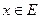Пр Ряд 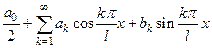, где

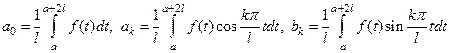
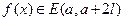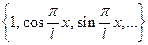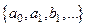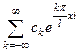называется тригонометрическим рядом Фурье функции по ортогональной системе с коэффициентами . Ряд , где 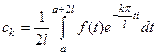, называется рядом Фурье в комплексной форме функции 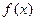по ортогональной системе 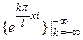с коэффициентами .

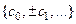Опр Член 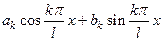называется 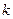- ой гармоникой тригонометрического ряда 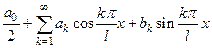. Если положить 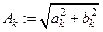и определить угол 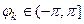из системы 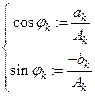, то 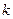-ю гармонику можно записать в виде .

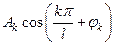Опр Пусть 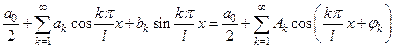есть тригонометриче ский ряд Фурье 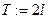-периодической функции 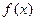. Последовательность 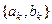или 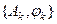называется спектром периодической функции 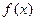; 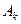- амплитудой 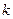- ой гармоники; 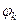- фазой 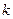- ой гармоники. 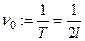- основная частота; 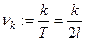- - 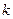ая гармоническая частота. 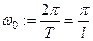- основная круговая частота; 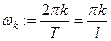- - 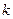ая круговая частота функции .

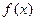ТЕОРЕМА 8.2 (свойства поточечной сходимости тригонометрического ряда Фурье) 1) Пусть 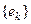ортонормированная последовательность в вещественном евклидовом пространстве 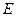. Для каждого элемента 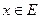существует единственный "многочлен" 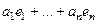степени 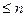, отклонение которого от элемента 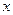будет наименьшим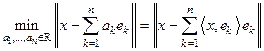. 2) Для каждого элемента 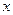гильбертова про-ва 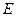его ряд Фурье сходится по норме 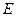. Для того, чтобы он сходился к самому элементу, необходимо и достаточно, чтобы имело место равенство Парсеваля 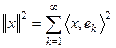. 3) Для функции 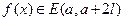ее тригонометрический ряд Фурье в каждой точке 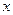сходится к числу 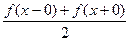. 4) В условиях предыдущего пункта 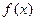представима в этом же смысле в виде ряда Фурье в комплексной форме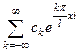, причем 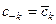и коэффициенты 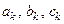связаны равенством 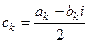. 5) Если функция 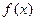четная (нечетная) на 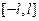и удовлетворяет условиям пункта 3), то 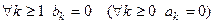, то есть она разлагается в ряд по косинусам (по синусам) на оси. При этом .

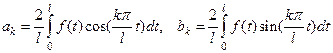◄ 4) ,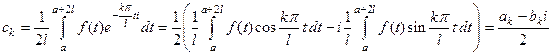

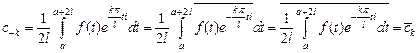. 5) Пусть, например, 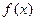является нечетной. Тогда 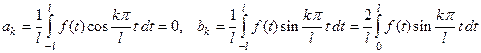в силу свойств определенного интеграла от четной и нечетной функций. Пункты 1)-3) без доказательства. ►

ЗАМЕЧАНИЕ (электротехнический смысл) Для функции 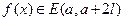равенство Парсеваля принимает вид 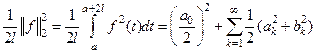. Для периодического с периодом 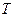на 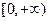аналогового сигнала (тока, напряжения) 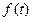величина 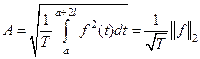называется квадратическим (действующим) значением сигнала. Нетрудно убедиться, что для 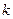-ой гармоники 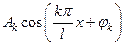такого сигнала квадрат действующего значения равен 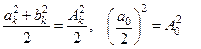. В этих обозначениях равенство Парсеваля принимает вид 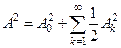. То есть квадрат действующего значения сигнала равен сумме квадратов действующих значений составляющих его гармоник.