ОпрЛогические формулы называются равносильными, если соответствующие им булевы функции совпадают

Обозначение Равносильность формул обозначается знаком =.

ЗАМЕЧАНИЕ (свойства унарных и бинарных операций):

1. Коммутативность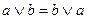
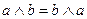
2. Ассоциативность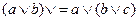
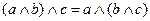
3. Дистрибутивность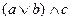
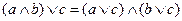
4. Закон де Моргана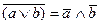
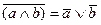
5. Свойства исключён ного третьего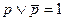
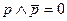
6. Закон поглощения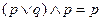
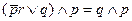
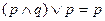
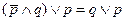
7. Свойства единицы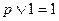
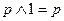
8. Свойства нуля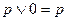
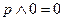
9. Свойства отрицания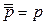
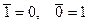
10.Свойство имплика- ции и эквивалентности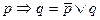
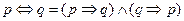
11.Сложение по моду- лю два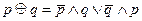

_____

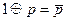
Опр Суперпозицией (композицией) функций называется сложная функция, составленная из этих функций.

ТЕОРЕМА 4 (Шеннона) Любая булева функция может быть представлена как суперпозиция трёх операций 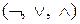над двоичными переменными.

◄ Докажем сначала тождество Шеннона: для любой булевой

функции .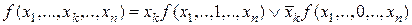

Действительно, при ,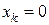

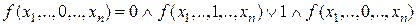а при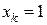

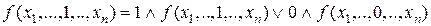
Применим эту формулу последовательно к переменным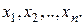

.

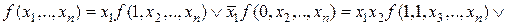
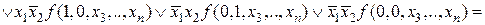
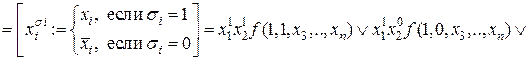
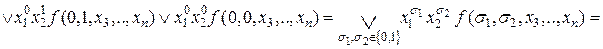
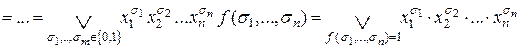Доказана формула Шеннона . ►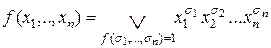

Опр Конъюнктом называется любая конъюнкция двоичных переменных или их отрицаний.

Пример .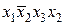

Опр Булева функция вида 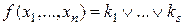, где 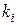- конъюнкты, называется дизъюнктивной нормальной формой (ДНФ).