Функциональные преобразователи и схемы

Опр Обозначим множество 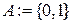. Отображение 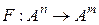называется функциональным преобразователем. Отображение 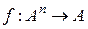называется двоичной (булевой) функцией от 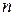двоичных переменных.

ЗАМЕЧАНИЕ 1 Функциональный преобразователь 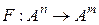является отображе нием 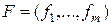, координатные функции которого есть булевы функции от 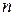переменных.

ЗАМЕЧАНИЕ 2 Существуют 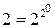постоянные булевы функци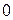и и 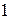. Булевы функции, не содержащие переменных называются нульарными.

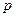
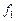
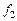
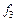
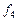
ЗАМЕЧАНИЕ 3 Существует 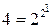булевых функции относительно одной двоичной переменной (унарные). Их табличное задание следующее:

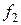– тождественная, 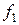, 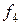- постоянные, 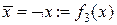- отрицание.

ЗАМЕЧАНИЕ 4 Существует 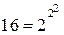булевых функций от двух двоичных переменных (бинарные операции):

											...
											.
											…
											…
											…

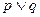
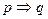
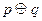
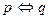
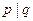
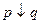
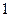
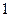
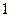
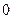
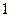
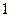
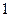
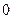
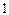
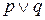- дизъюнкция; 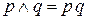- конъюнкция; 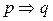- имплика ция; 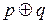- сложение по модулю два; 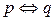- эквиваленция; 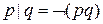- штрих Шеффера; 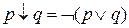- стрелка Пирса.

ЗАМЕЧАНИЕ 5 Существует 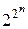булевых функций от 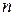двоичных переменных.

Опр Булева функция задаваемая в виде упорядоченной системы унарных и бинарных операций над входящими в неё двоичными переменными и постоянными 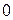, , 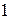называется логической формулой (переключательной функцией).

ЗАМЕЧАНИЕ Приоритет выполнения операций в логической формуле задаётся с помощью скобок, а также в следующей последовательности: 1) отрицание; 2) конъюн кция; 3) дизъюнкция; 4) все остальные бинарные операции, при этом оследовательно-

сть их выполнения также должна регулироваться скобками.

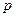
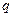
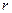
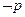
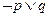
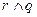
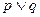
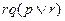
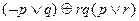
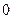
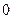
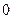
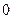
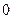
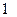
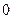
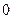
Пример Логическая формула 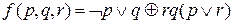имеет такое табличное задание

ЗАМЕЧАНИЕ Булевы функции могут задаваться аналитически, графически, таблич но, в векторной форме и в виде логических схем.

Опр Логическая формула называется тавтологией (тождественно-ложной), если порождаемая ею булева функция тождественно равна единице (нулю).