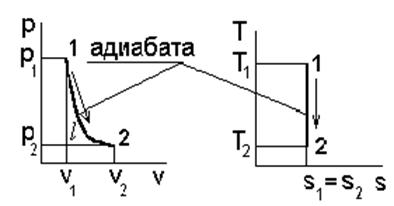
Рис. Адиабатный процесс 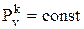 ,
, 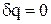
Адиабатный процесс протекает без теплообмена с окружающей средой, при соблюдении условия dq=0. Из выражения () при условии dq=0 следует 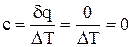 , т.е. теплоемкость адиабатного процесса с=0. Из ()
, т.е. теплоемкость адиабатного процесса с=0. Из () 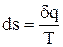 вытекает, что ds=0, s=const Следовательно, в адиабатном процессе энтропия не изменяется. В соответствии с выражением
вытекает, что ds=0, s=const Следовательно, в адиабатном процессе энтропия не изменяется. В соответствии с выражением 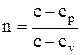 показатель политропы при адиабатном процессе будет равен
показатель политропы при адиабатном процессе будет равен 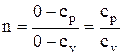 , который обозначается
, который обозначается 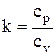 , как было отмечено выше, и называется показателем адиабаты. Уравнение, описывающее адиабатный процесс, имеет вид p·vk=const, из которого следует
, как было отмечено выше, и называется показателем адиабаты. Уравнение, описывающее адиабатный процесс, имеет вид p·vk=const, из которого следует 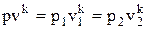 .
.
Перечень величин при адиабатном процессе должен удовлетворять следующим соотношениям:
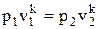 ; (1.56)
; (1.56)
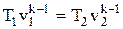 ;
;
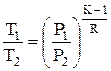 ;
;
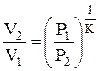 ;
;
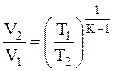 ; (1.57)
; (1.57)
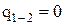
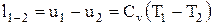 ; (1.58)
; (1.58)
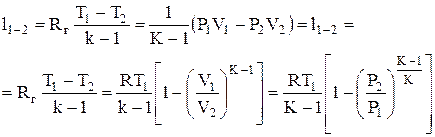 (1.59)
(1.59)
Du=u2 -u1=cv(T2 -T1); (1.60)
Dh=h2 -h1=cp(T2 -T1); (1.61)
Ds=s2-s1=0, т. к. s2= s1. (1.62)
Политропные процессы 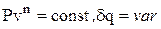
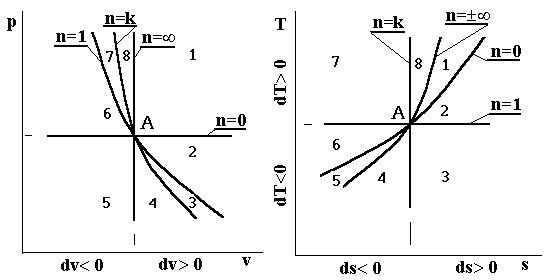
Рис.
Выше было отмечено, что термодинамические процессы, которые описываются уравнением p×vn=const, называются политропными. В этом уравнении показатель политропы меняется в пределах -¥< n< +¥. Представим объединенную картину линий изопараметрических процессов в pv -, Ts - диаграммах, приняв за начало всех процессов (как в сторону расширения, так и в сторону сжатия) произвольную точку А. На рис. приведены соответственно: изохора (n= ±¥), изобара (n=0), изотерма (n=1), адиабата (n=k). Эти изолинии делят координатную плоскость на 8 областей, в пределах каждой из которых все термодинамические процессы обладают общностью определенных свойств. Все процессы, начинающиеся в точке А и происходящие в областях 1, 2, 3, 4, сопровождаются расширением рабочего тела (dv>0), следовательно, при этом совершается положительная работа δl=p×dv, а процессы, происходящие в областях 5, 6, 7 и 8 (dv<0), имеют отрицательную работу (в этих случаях работа совершается над системой внешними силами).
Процессы, совершающиеся в областях 1, 2, 3 и 8, протекают с подводом теплоты извне (ds>0), а в областях 4, 5, 6 и 7 - с отводом теплоты (ds<0).
Изотерма (n=1) делит рассматриваемое поле координатной плоскости на две части: в областях 1, 2, 7, 8 процессы протекают с повышением температуры (dT>0), а в областях 3, 4, 5, 6 процессы протекают с понижением температуры (dT<0). В области 3 между изотермой (n=1) и адиабатой (n=k) при подводе теплоты (ds>0) происходит падение температуры (dT<0), а при отводе теплоты (ds<0) в области 7 происходит повышение температуры (dT>0).
Все соотношения, вытекающие из уравнений политропных процессов p×vn=const; T×vn-1=const; Tn×p1-n=const, должны быть аналогичными соотношениям, вытекающим из соответствующих уравнений адиабатного процесса и получаются путем замены показателя адиабаты k на показатель политропы n. Однако при этом необходимо иметь в виду, что теплоемкость политропного процесса определяется по формуле 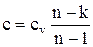 , а также теплота, участвующая в процессе, в этом случае определяется исходя из уравнения первого закона термодинамики
, а также теплота, участвующая в процессе, в этом случае определяется исходя из уравнения первого закона термодинамики
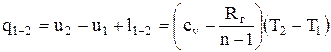 .
.
Перечень величин (*) в политропном процессе должен удовлетворять следующим соотношениям:
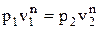 ; (1.63)
; (1.63)
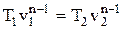 ; (1.64)
; (1.64)
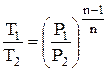 ;
; 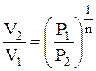 ;
; 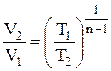 (1.65)
(1.65)
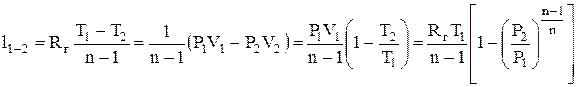 ; (1.66)
; (1.66)
Du=u2 -u1=cv×(T2-T1); (1.67)
Dh=h2 -h1=cp× (T2-T1); (1.68)
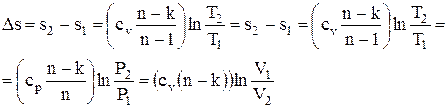 ; (1.69)
; (1.69)

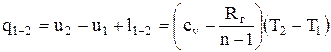 . (66)
. (66)
 2014-02-24
2014-02-24 1549
1549
