Система п уравнений с п неизвестными.
Систему линейных уравнений можно записать в матричной форме, для этого введем обозначения:
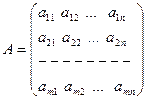 - матрица коэффициентов при неизвестных;
- матрица коэффициентов при неизвестных;
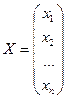 - матрица-столбец переменных;
- матрица-столбец переменных;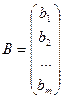 - матрица-столбец свободных членов. Теперь систему можно записать в виде:
- матрица-столбец свободных членов. Теперь систему можно записать в виде: 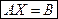 .
.
Матрица 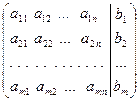 называется расширенной матрицей системы уравнений.
называется расширенной матрицей системы уравнений.
Пусть число уравнений системы равно числу переменных, т.е. 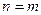 . Тогда матрица системы является квадратной, а её определитель
. Тогда матрица системы является квадратной, а её определитель 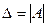 является определителем системы.
является определителем системы.
Для получения решения системы при 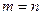 предположим, что квадратная матрица системы
предположим, что квадратная матрица системы 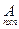 невырожденная, т.е. ее определитель
невырожденная, т.е. ее определитель 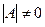 . В этом случае существует обратная матрица
. В этом случае существует обратная матрица 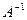 .
.
Умножая слева обе части матричного равенства на матрицу 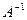 , получим
, получим 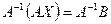 . Т.к.
. Т.к. 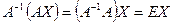 , то решением системы методом обратной матрицы будет матрица–столбец
, то решением системы методом обратной матрицы будет матрица–столбец
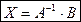
 2014-02-24
2014-02-24 801
801








