Обратная матрица

Для любого действительного числа 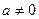существует обратное число 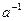такое, что 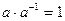. Для квадратных матриц вводится аналогичное понятие.

· Определение. Матрица 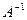называется обратной по отношению к квадратной матрице 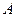, если при умножении этой матрицы на обратную, как справа, так и слева получается единичная матрица:

.

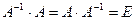Из определения следует, что только квадратная матрица имеет обратную; при этом обратная матрица также является квадратной того же порядка. Однако не каждая квадратная матрица имеет обратную.

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 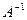существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная .

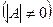Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если 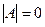, то матрица 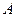- вырожденная и не имеет обратной матрицы.
2. Находим матрицу 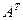- транспонированную к матрице .
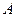3. Находим алгебраические дополнения элементов транспонированной матрицы 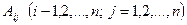и составляем из них матрицу, заменяя каждый элемент матрицы 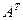его алгебраическим дополнением. Такая матрица называется присоединенной (или союзной), обозначим ее .
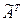4. Вычисляем обратную матрицу по формуле .
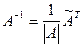5. Проверяем правильность вычисления обратной матрицы 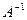, исходя из её определения: .

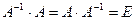Пример 1. Найти матрицу, обратную данной .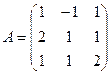

1. Найдем определитель матрицы 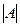разложением по первой строке 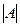=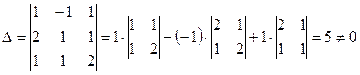, следовательно, матрица А невырожденная и обратная матрица существует.
2. Находим матрицу 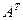, транспонированную к А: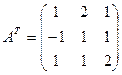
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу:

.

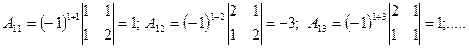
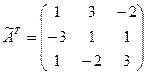1. Вычисляем обратную матрицу.
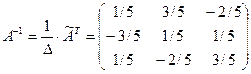2. Проверяем правильность вычисления обратной матрицы по формулам: 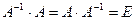(выполнить самостоятельно).