Теорема Крамера. Пусть 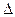 - определитель матрицы системы А, а
- определитель матрицы системы А, а 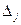 - определитель матрицы, получаемой из матрицы А заменой
- определитель матрицы, получаемой из матрицы А заменой 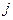 -го столбца столбцом свободных членов. Тогда, если
-го столбца столбцом свободных членов. Тогда, если 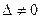 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам: 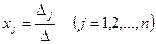 .
.
Эти формулы получили название формул Крамера.
Из рассмотрения формул ясно, что при 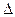 =0 система или не имеет решения (если один из определителей
=0 система или не имеет решения (если один из определителей 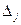
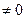 ), или имеет бесчисленное множество решений при всех
), или имеет бесчисленное множество решений при всех 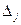 =0.
=0.
Заметим: 1. Если система однородна, т.е. все свободные члены равны нулю, то она всегда имеет нулевое (тривиальное) решение при 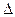
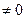 ;
;
2. Если 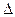 =0, то однородная система имеет ненулевые решения.
=0, то однородная система имеет ненулевые решения.
Существенным недостатком решения систем 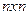 методом Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не применяются для решения экономических задач, сводящихся часто к системам с большим числом неизвестных.
методом Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не применяются для решения экономических задач, сводящихся часто к системам с большим числом неизвестных.
Элементарные преобразования системы линейных уравнений, не нарушающие равносильность системы:
1) Вычеркивание уравнения системы, у которой все коэффициенты при неизвестных и свободный член равны нулю. Такое уравнение называется тривиальным.
2) Умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
3) Замена 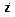 -го уравнения системы уравнением, которое получается путем почленного сложения
-го уравнения системы уравнением, которое получается путем почленного сложения 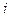 -го и
-го и 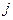 -го уравнений системы.
-го уравнений системы.
Пример. Решим систему 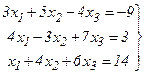
методом Крамера.
Определитель данной системы
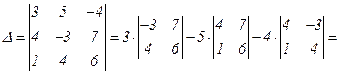
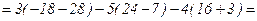
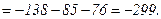
Вычислим определители 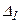 ,
, 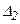 и
и 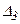 :
:
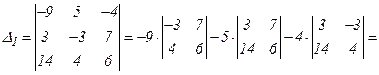
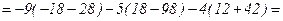
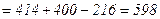 .
.
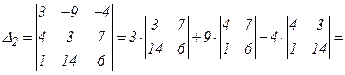
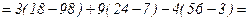
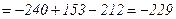 .
.
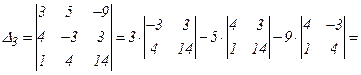
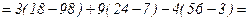
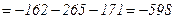 .
.
Решение системы: 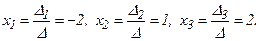
Для того чтобы убедиться в правильности решения, сделаем проверку, то есть подставим найденные значения 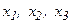 в исходную систему
в исходную систему
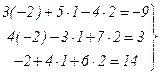 .
.
 2014-02-24
2014-02-24 2233
2233
