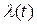Выбор количественных характеристик надежности зависит от типа объекта. Наиболее целесообразно разбить все основные показатели надежности на две группы: для невосстанавливаемых и для восстанавливаемых объектов. При этом показатели надежности рассматриваются и как вероятностные характеристики, и как статистические характеристики.
Вероятность безотказной работы 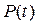
Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находился в работоспособном состоянии.
Согласно определению
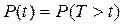 , (1.1)
, (1.1)
где t – время, в течение которого определяется вероятность безотказной работы; Т – время работы объекта от его включения до первого отказа.
Для рассмотрения статистических определений показателей надежности невосстанавливаемых систем предполагается, что на испытании находится N0 одинаковых объектов, условия испытания одинаковы, а испытания каждого из объектов проводятся до его отказа.
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением
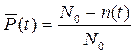 , (1.2)
, (1.2)
где N0 – число объектов в начале испытания; n(t) – число отказавших объектов за время t; 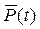 – статистическая оценка вероятности безотказной работы. При большом числе объектов N0 статистическая оценка
– статистическая оценка вероятности безотказной работы. При большом числе объектов N0 статистическая оценка 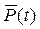 практически совпадает с вероятностью безотказной работы
практически совпадает с вероятностью безотказной работы 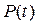 . На практике иногда более удобной характеристикой является вероятность отказа Q(t).
. На практике иногда более удобной характеристикой является вероятность отказа Q(t).
Вероятностью отказа Q(t) называется вероятность того, что при определенных условиях эксплуатации в заданном интервале времени возникнет хотя бы один отказ. Отказ и безотказная работа являются событиями несовместными и противоположными, поэтому
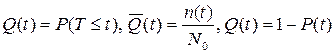 (1.3)
(1.3)
Плотность распределения f(t) (частота отказов) – плотность распределения наработки до отказа. Согласно вероятностному определению:
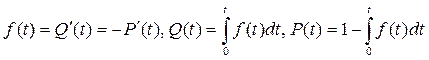 (1.4)
(1.4)
При наблюдении за работой N0 объектов можно определить плотность распределения как отношение числа отказавших в единицу времени объектов к общему числу объектов при условии, что отказавшие объекты не восстанавливаются:
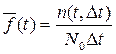 , (1.5)
, (1.5)
где 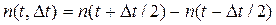 - число отказавших объектов в интервале
- число отказавших объектов в интервале 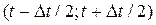 .
.
Вероятностная оценка этой характеристики находится из выражения:
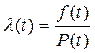 (1.6)
(1.6)
Для статистического определения интенсивности отказов получим
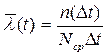 , (1.7)
, (1.7)
где 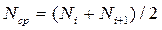 – среднее число исправно работающих объектов в интервале
– среднее число исправно работающих объектов в интервале 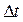 ;
; 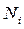 – число объектов, исправно работающих в начале интервала
– число объектов, исправно работающих в начале интервала 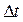 ;
; 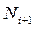 – число изделий исправно работающих в конце интервала
– число изделий исправно работающих в конце интервала 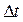 .
.
Средняя наработка до отказа 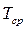
Согласно определению
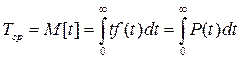 , (1.8)
, (1.8)
где M – символ математического ожидания.
По статистическим данным об отказах средняя наработка до отказа вычисляется по формуле
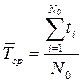 , (1.9)
, (1.9)
где 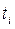 – время безотказной работы i- го образца;
– время безотказной работы i- го образца; 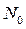 – число испытуемых образцов.
– число испытуемых образцов.
Как видно из формулы (1.9), для определения средней наработки до отказа необходимо знать моменты выхода из строя вcex испытуемых элементов. Поэтому для вычисления 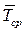 пользоваться указанной формулой неудобно. Имея данные о количестве вышедших из строя элементов
пользоваться указанной формулой неудобно. Имея данные о количестве вышедших из строя элементов 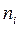 в каждом i -м интервале времени, среднюю наработку до отказа лучше определять по формуле
в каждом i -м интервале времени, среднюю наработку до отказа лучше определять по формуле
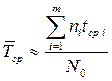 (1.10)
(1.10)
В выражении (1.10) 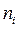 и m находятся по следующим формулам:
и m находятся по следующим формулам:
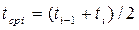 ,
, 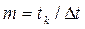 ,
,
где 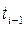 – время начала i -го интервала;
– время начала i -го интервала; 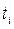 – время конца i -го интервала;
– время конца i -го интервала; 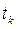 – время, в течение которого вышли из строя все элементы;
– время, в течение которого вышли из строя все элементы; 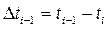 – интервал времени.
– интервал времени.
Взаимосвязь показателей безотказности невосстанавливаемых объектов показана в таблице 1.1.
Таблица 1.1
| Характеристики |  | 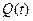 | 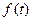 | 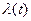 |
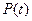 | - | 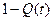 | 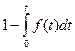 | 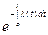 |
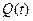 | 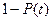 | - | 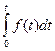 | 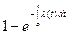 |
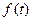 | 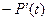 | 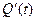 | - | 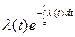 |
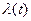 | 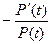 | 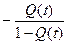 | 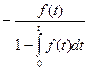 | - |
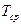 | 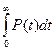 | 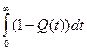 | 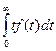 | 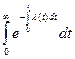 |
Рассмотренные критерии надежности позволяют достаточно полно оценить надежность невосстанавливаемых объектов. Они также позволяют оценить надежность восстанавливаемых объектов до первого отказа. Наличие нескольких критериев не означает, что всегда нужно оценивать надежность изделий по всем критериям.
Наиболее полно надежность изделий характеризуется частотой отказов f(t). Это объясняется тем, что частота отказов является плотностью распределения, а поэтому несет в себе всю информацию о случайном явлении – времени безотказной работы.
Средняя наработка до первого отказа является достаточно наглядной характеристикой надежности. Однако применение этого критерия для оценки надежности сложной системы ограничено в тех случаях, когда:
- время работы системы гораздо меньше среднего
времени безотказной работы;
- закон распределения времени безотказной работы
не однопараметрический и для достаточно полной оценки
требуются моменты высших порядков;
- система резервированная;
- интенсивность отказов непостоянная;
- время работы отдельных частей сложной системы
разное.
Интенсивность отказов – наиболее удобная характеристика надежности простейших элементов, так как она позволяет более просто вычислять количественные характеристики надежности сложной системы.
Наиболее целесообразным критерием надежности сложной системы является вероятность безотказной работы. Это объясняется следующими особенностями вероятности безотказной работы:
- она входит в качестве сомножителя в другие, более
общие характеристики системы, например в эффективность и стоимость;
- характеризует изменение надежности во времени;
- может быть получена сравнительно просто расчетным путем в процессе проектирования системы и оценена в процессе ее испытания.
 2014-02-09
2014-02-09 6549
6549