Математическая формулировка задач целочисленного программирования аналогична задачам нелинейного программирования:
|
Однако специфика задач целочисленного программирования заключается в том, что переменные xj и функции F(х), φi(x) могут принимать только дискретные значения. Специальными преобразованиями в подавляющем большинстве случаев можно свести эти дискретные значения к целочисленным.
В общем случае целочисленными могут быть не все, а части переменных и функций. Иногда целочисленное программирование называется дискретным программированием. Однако, как уже указывалось выше, при полном рассмотрении всех методов оптимизации оказывается, что этот термин уже используется в другом смысле.
Если все функции F(х), φi(x) в задаче (3.10) линейные, то имеет место линейная задача целочисленного программирования. Методы решения таких задач получили наибольшее распространение. Очевидно, что могут встречаться задачи с целочисленными переменными xj и функциями F(х), φi(x) и целочисленными переменными и непрерывными функциями (рис. 3.6). Как правило, именно этот последний случай рассматривается в большинстве руководств. Кроме того, встречаются задачи частично и полностью целочисленные в зависимости от того, часть или все переменные xj принимают целочисленные значения. Как уже отмечалось, допустимые дискретные значения, входящие во множество, могут быть даже нецелочисленными. В частности, это множество может быть бесконечным, конечным или даже состоящим всего из двух значений: 0 и 1. В этом случае имеет место целочисленное программирование с булевыми переменными, методы которого в значительной мере перекрываются логическим синтезом конечных автоматов.
Методы целочисленного программирования значительно отличаются от методов оптимизации, рассмотренных ранее, и по существу своему относятся к дискретной математике. Они не обладают таким единством, как методы вариационного исчисления, и в большинстве представляют собой набор частных приемов, пригодных для решения частных задач. Однако актуальность этих методов требует их дальнейшего развития и совершенствования, так как наиболее важные прикладные задачи типа оперативно-календарного планирования сводятся к задачам целочисленного программирования.
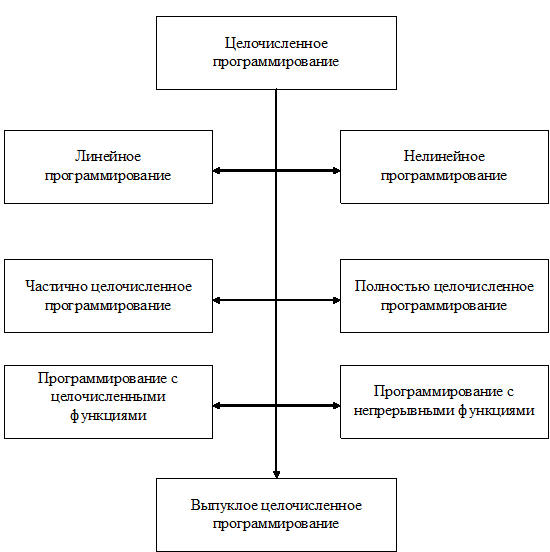
Рис. 3.6. Классификация задач целочисленного программирования
Со значительными оговорками все методы решения задач целочисленного программирования можно разделить на четыре группы (рис. 3.7):
– методы отсечения;
– комбинаторные методы;
– приближенные методы;
– другие методы, которые нельзя отнести ни к одной из трех первых групп.
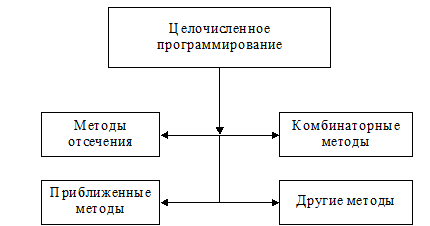
Рис. 3.7. Классификация методов решения задач целочисленного программирования
Первая группа использует процедуру линейного программирования для последовательности задач, в которые постепенно вводятся линейные ограничения, и тем самым реализуется процесс правильного отсечения. Основу всех методов этой группы составляют три алгоритма Гомори и их модификации.
Большинство комбинаторных методов не используют симплекс-методы, а достигают сокращения поиска оптимальных значений анализом исходного множества.
Дискретное динамическое программирование по-прежнему успешно применяется для решения задач целочисленного програмирования и в приведенной на рис. 3.7 классификации содержится в разделе комбинаторных методов, так как по существу оно является направленным методом перебора. Значительно реже используется дискретный принцип максимума. Широкие возможности в части решения прикладных задач большой размерности открываются при использовании человеко-машинных методов оптимизации. По своей идеологии эти методы примыкают к лингвистическим с добавлением блоков эвристики, в качестве которых выступает человек при общении с ЭВМ.
Характерная особенность общей задачи целочисленного программирования заключается в ее нерегулярности. Под регулярностью понимают совокупность необходимых и достаточных условий экстремума, которые позволяют создать конечную процедуру его отыскания. Условиям регулярности удовлетворяют задачи линейного и выпуклого программирования. В регулярных задачах локальный экстремум совпадает с глобальным. Указанные выше обстоятельства определяются характером области допустимых значений, которая становится многосвязной из-за требования целочисленности (дискретности), а также невыпуклой. Несовпадение целочисленного и нецелочисленного экстремумов рассматривается в следующем примере.
Пример. Требуется найти решение следующей задачи целочисленного программирования:
1/2x1 – x2 ³ 2;
1/5x1 + x2 ³ 3;
x1 – 1/3x2 ³ 4;
x1, x2 ³ 0;
max z = 1/5x1 + x2.
При целочисленности переменных максимум zопт = 13/5 достигается в точке х1опт = 3, х2опт = 2, в то время как при исключении этого требования zопт = 3 в точке х1опт = 10/7, х2опт = 19/7. Округление результата до целых не дает оптимума исходной задачи, как это видно из рис. 3.8. Заметим, что условие целочисленности z при снятии этого требования к переменным х1 и х2 определяет оптимум при других значениях х1 и х2.
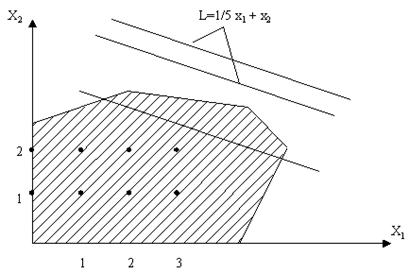
Рис. 3.8. К особенностям задач целочисленного программирования
Из этого простейшего примера виден комбинаторный характер задач целочисленного программирования, который часто требует прямого перебора. Задача дискретного нецелочисленного программирования может быть сведена к задаче целочисленного программирования. Допустим, имеется задача математического программирования в виде
min{F(x)|xj ³ 0; j = 1, 2,..., n; φi(x) ≤ 0; i = 1, 2,..., m}.
Будем считать, что переменная xj0 может принимать только одно из заданного множества значений
xj0 Ì {kj01, kj02,..., kj0p}.
Введем дополнительные булевы переменные у1, y2,..., yp и запишем условие дискретности для xj0 в виде:
|
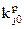 yp;
yp;
yj = 1 или 0, j = 1, 2,..., p;
у1 + y2 +... + yp = 1.
Последнее соотношение требует, чтобы только одна переменная уv была отлична от нуля. Нетрудно убедиться, что формулы (3.11) обеспечивают дискретность переменной xj0. Таким образом, путем введения булевых переменных уv можно всегда свести нецелочисленную дискретную задачу математического программирования к целочисленной. Как видно, соотношения (3.11) представляют собой p-кратную логическую альтернативу:
<<xj0 = k01, или xj0 = k02, или..., или xj0 = k0p>>.
Для лучшего понимания связи задач целочисленного программирования с задачами на многосвязных и невыпуклых областях покажем, как эти последние сводятся к задачам целочисленного программирования. Пусть допустимая область изменения переменной xj0 многосвязная и задается соотношениями:
0 ≤ xj0 ≤ kj0;
|
0 ≤ a< b≤ kj0.
Введем дополнительную булеву переменную yj0, которую не будем включать в функцию цели, а заменим рассмотренные соотношения следующими:
|
-xj0 + ayj0 + kj0(1– yj0) ≤ 0;
yj0 = 1 или 0.
Очевидно, что соотношения (3.11а) и (3.11б) эквивалентны. Действительно, когда yj0 = 1, то (3.11б) сводится к xj0 ³ 0 и xj0 ≤ a; когда yj0 = 0, то xj0 ³ b и xj0 ≤ kj0. Таким образом, многосвязность области допустимых значений легко учитывается введением дополнительных булевых переменных. Этот метод без труда распространяется на случай многих переменных.
Процедура сведения невыпуклой области изменения переменных к стандартным ограничениям состоит в следующем. Область разбивается на выпуклые подобласти, и между некоторыми парами их вводятся альтернативные условия (дизъюнкции). Для каждой подобласти определяется верхняя граница, и вводятся дополнительные ограничения, включающие для каждой пары подобластей булевы переменные.
Пример. Рассмотрим процедуру сведения задачи невыпуклого программирования к целочисленному программированию. Пусть область допустимых значений задана системой неравенств:
x1 + 1/4x2 ≤ 2;
2/5x1 – x2 ³ –1;
x1 – 1/3x2 ≤ 3;
x1, x2 ³ 0.
Соответствующая область представлена на рис. 3.9. Первая и вторая пара неравенств образуют выпуклые подобласти x1, x2 с учетом неотрицательности переменных с верхними границами x1макс, x2макс, соответственно. Введение булевой переменной у приводит к дополнительным неравенствам:
x1 – yxмакс ≤ 0;
x2 – (1 – y)xмакс ≤ 0.
Здесь каждое условие относится ко всем неравенствам соответствующей области.
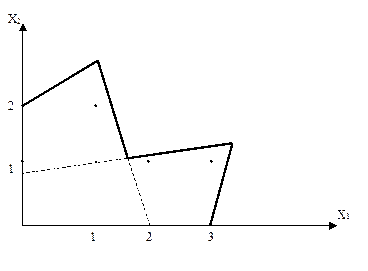
Рис.3.9. Невыпуклая область, состоящая из выпуклых многогранников
Нетрудно убедиться, что аналогичный способ применим в случае числа переменных, большего двух.
 2014-02-24
2014-02-24 2466
2466
