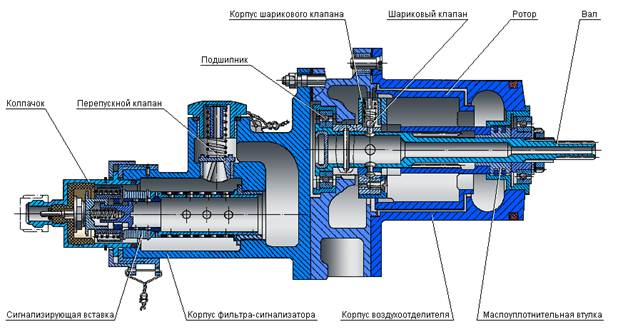
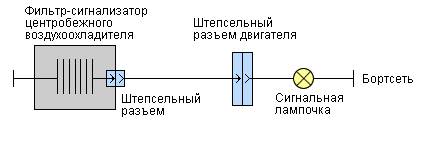
ЭЛЕКТРИЧЕСКАЯ СХЕМА ПОДСОЕДИНЕНИЯ ФИЛЬТРА-СИГНАЛИЗАТОРА СТРУЖКИ
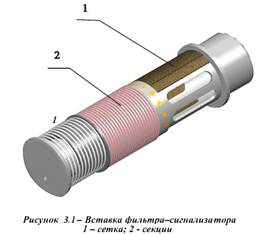
Сигнализатор стружки в составе ЦВС-30

Нелинейное программирование включает в себя методы определения минимума функции n переменных F(х), где х = ||x1,x2,...,xn|| при m+n ограничивающих условиях:
φi(x) ≤ 0, i = 1,..., m;
|
|
φ ≤ 0, x ³ 0.
Соотношения (3.2) следует понимать таким образом, что каждая компонента векторов φ и х в них не менее нуля. Иногда сокращенно соотношения (3.1) и (3.2) записывают в виде
min{F(x)|xj ³ 0, j = 1,..., n; φi(x) ≤ 0, i = 1,..., m}
или
min{F(x)| x Ì G},
где область G задается условиями
G = { x | x ³ 0, φ i(x) ≤ 0 для всех i}.
В нелинейном программировании допускаются в общем случае любые соотношения между n и m, т.е. n > m, n = m, m < n.
В задачах нелинейного программирования, так же как и в задачах линейного программирования, могут встречаться другие формы написания условий. Но все возможные формы могут быть сведены к виду (3.1), который в дальнейшем будем называть нормальным.
В общем случае функции F(х) и φ i(x) бывают произвольными и, в частности, линейными. Задачи, решаемые прямыми методами поиска, являются частными случаями задач вида (3.1), (3.2).
Задачи поиска экстремума функции при наличии ограничений можно решать с помощью классических методов, но они рассматривают только случаи, когда неравенства имеют вид строгих равенств
F(х) → min;
φi(x) = 0.
При этом не требуется неотрицательности переменных хj, m<n, а функции F(х) и φ i(x) непрерывны и имеют частные производные. Для нелинейного программирования классические методы имеют большое теоретическое значение, так как основополагающая теорема Куна-Таккера в выпуклом программировании обобщает теорему Лагранжа для классических задач. В начале будут рассмотрены классические методы отыскания экстремума функции с ограничениями.
Основной недостаток методов нелинейного программирования заключается в том, что с их помощью не всегда удается найти глобальный экстремум при наличии нескольких локальных экстремумов. Определить глобальный экстремум можно лишь методом динамического программирования. Однако его применение зависит от определенных условий, обеспечивающих выполнение принципа оптимальности Беллмана. Решение задач нелинейного программирования методом динамического программирования имеет свою специфику, благодаря которой динамическое программирование часто рассматривают в разделе нелинейного программирования. Применение дискретного принципа максимума Понтрягина для решения задач нелинейного программирования менее разработано, чем применение динамического программирования, так как этот метод более “чувствителен” к введению ограничений на переменные.
Теоретически нелинейное программирование разработано только для одного частного случая выпуклых функций F(х) и φi(x), и соответственно этот раздел назван выпуклым программированием (рис. 3.1).
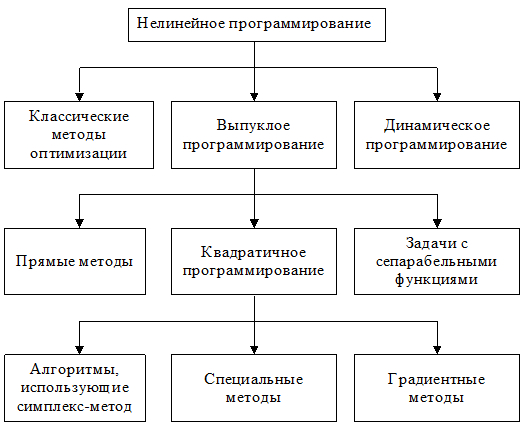
Рис. 3.1. Классификация методов нелинейного программирования
Функция f(х) n переменных ||x1,..., xn|| = x Ì G называется выпуклой функцией в выпуклой области G, если для любых двух точек из G выполняется соотношение
|
где 0 ≤ l ≤ 1. Функция будет строго выпуклой, если здесь знак “≤” можно заменить на “<“. Соотношение (3.3) означает, что выпуклая функция не может принимать больших значений, чем линейная функция, интерполирующая значения f(х 1) и f(х 2). На рис. 3.2 приведен пример выпуклой функции одной переменной.
Соответственно функция f(х) называется вогнутой (или строго вогнутой), если функция [-f(х)] выпукла (строго выпукла).
Следует заметить, что определение вогнутости и выпуклости может показаться на первый взгляд неправильным. Например, тарелка, стоящая на столе, считается вогнутой, но если рассматривать ее с точки зрения нашего определения, т.е. при направлении третьей оси вверх, она выпукла. Дело в том, что обычное понятие выпуклости всегда совпадает с математическим, если смотреть по положительному, а не по отрицательному направлению оси, относительно которой определяется выпуклость. В примере с тарелкой на столе на нее следует смотреть снизу стола, тогда она будет выпуклой. Заметим, что для выпуклых функций (см. рис. 3.2)
d2f(x)/dx2 ³ 0.
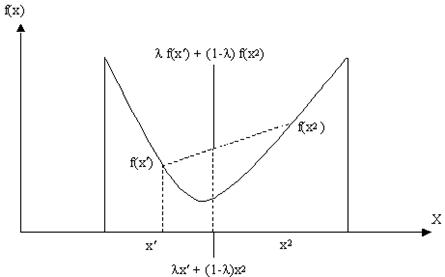
Рис. 3.2. К определению выпуклой функции
Метод считается теоретически разработанным, если найдены соотношения, являющиеся необходимыми и достаточными условиями оптимума, и алгоритмы поиска экстремума с доказательством их сходимости. Этим требованиям, строго говоря, удовлетворяют только методы, рассматриваемые в разделе квадратичного программирования, частично методы решения задач с сепарабельными функциями и в значительно меньшей степени – прямые методы. Функция f(х) = = f(x1,..., xn) называется сепарабельной, если она представлена в виде
f(x1,..., xn) = 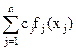 = c1f1(x1) + c2f2(x2) +... + cnfn(xn).
= c1f1(x1) + c2f2(x2) +... + cnfn(xn).
В общем случае эти функции не являются выпуклыми. Однако если каждая из функций fj(xj) выпуклая и коэффициенты cj неотрицательны, то функция f(х) тоже выпуклая. Методы решения задач с сепарабельными функциями, основанные на замене нелинейных функций ломаными кривыми, составленными из отрезков прямых, ищут локальный экстремум и не гарантируют отыскания глобального экстремума.
Теоретически наиболее широко и детально в нелинейном программировании разработан раздел выпуклого программирования, называемый квадратичным программированием, в котором функции представляются в виде суммы линейной и квадратичной форм и имеют вид
|
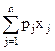 +
+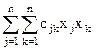 = p1x1 +...+ pnxn + c11x21 + c12x1x2 +...+ c1nx1xn + cnnx2n.
= p1x1 +...+ pnxn + c11x21 + c12x1x2 +...+ c1nx1xn + cnnx2n.
Для выпуклости необходимо, чтобы матрица C = ||cjk|| представляла собой симметричную матрицу, т.е. чтобы для любых х выполнялись условия симметрии cjk = ckj, и неотрицательно определенную xCx ³ 0.
Методы квадратичного программирования можно разделить на три группы:
– алгоритмы, использующие симплекс-метод;
– градиентные методы;
– специальные методы.
Отличие градиентных методов, рассматриваемых в квадратичном программировании, от рассмотренных в разделе прямых методов заключается в том, что в первом случае благодаря заданию функций в виде (3.4) удается получить значительно больше результатов, характеризующих конкретный метод. В прямых методах поиска, в градиентных и других алгоритмах, как правило, функция цели считается выпуклой (в большинстве случаев она задана аналитически, в виде таблиц или другим способом). Прямые методы по традиции много внимания уделяют аспектам поиска в условиях неопределенности, выбору, в каждом случае, оптимальной стратегии поиска.
а)
б)
в)
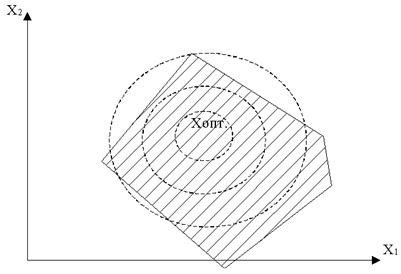
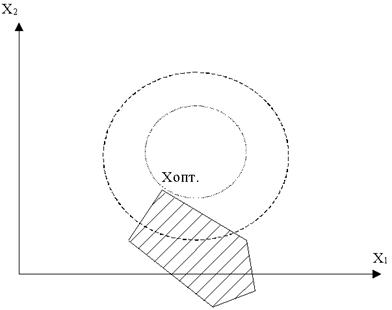
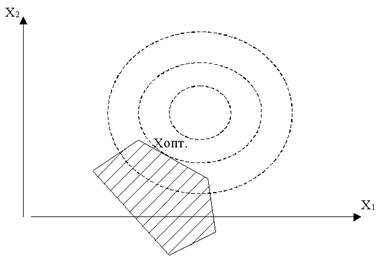
Рис. 3.3. Различные случаи оптимума в задачах нелинейного программирования
Задачи нелинейного программирования по сравнению с задачами линейного программирования обладают большим многообразием. На рис. 3.3 представлены возможные варианты расположения точки экстремума для случая двух переменных. Так, в случае линейных ограничений и нелинейной функции цели экстремума можно достигнуть в крайней точке (вершине) допустимой области значений (рис. 3.3, а), в одной из точек, лежащих на ограничивающих прямых (рис. 3.3, б), и, наконец, в точке, расположенной внутри области (рис. 3.3, в). Пунктирные концентрические окружности изображают линии постоянных значений функции цели, сплошные линии – границу области допустимых значений. На рис. 3.3, б экстремум определяется как точка касания прямой, ограничивающей допустимую область значений, и линии равных значений функции цели.
Решение задач нелинейного программирования может давать два или более экстремума, тогда как решение задач линейного программирования дает один экстремум. На рис. 3.4 показан случай, соответствующий линейным ограничениям и нелинейной (квадратичной) функции цели, где она достигает максимального значения в двух точках: А (локальный максимум) и В (глобальный максимум). На этом рисунке пунктиром обозначены постоянные значения функции цели F = const = Ci, сплошной линией ограничена область допустимых значений. При нелинейных ограничениях может иметь место случай многосвязной области допустимых значений, и в каждой изолированной подобласти функция цели может достигать своего одного или нескольких локальных экстремумов. На рис. 3.5 представлен случай двусвязной области, в которой функция цели достигает локальных экстремумов. Максимум в точке В – глобальный для всей области допустимых значений, в точке А – локальный.
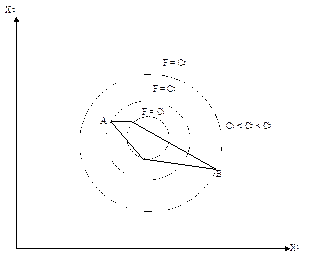
Рис. 3.4. Два экстремума при односвязной области допустимых значений
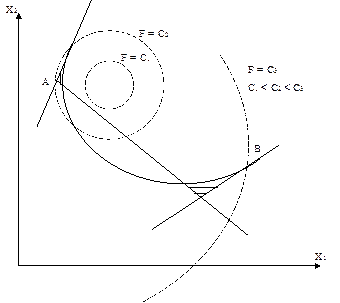
Рис. 3.5. Два экстремума при двусвязной области допустимых значений
 2014-02-24
2014-02-24 2006
2006