Нелинейное и целочисленное программирование

Можно показать, что любая задача выпуклого нелинейного программиро­вания может быть приближенно сведена к соответствующей задаче целочисленного программирования. Допустим, что функция цели F(х) имеет вид сепарабельной функции

(3.12)

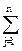F(x₁, x₂,..., x_n) = F_j(x_j).

(3.13)

Будем считать, что каждое слагаемое F_j(x_j) представляет собой выпуклую функцию, и в дальнейшем изложении опустим индекс j, используя обозначение F(х). Разобьем весь интервал изменения х на участки Δ_k = [d_k–1, d_k] длиной h_k = d_k – d_k–1. Если ввести новые переменные, равные длине пересечения отрезка [0, х] с отрезком Δ_k, т.е.

0 ≤ y_k ≤ h_k, k = 1, 2,..., p,

то

x = y₁ + y₂ +...+ y_p.

(3.14)

При этом функция F(х) может быть приближенно заменена на

F~(х) = c₀ + c₁y₁ + c₂y₂ +...+ c_py_p.

(3.15)

Для выпуклой функции F(х) коэффициенты С образуют монотонную последовательность

c₁ ≤ c₂ ≤... ≤ c_p.

Задача минимизации функции F(х), задаваемой формулой (3.14) при условиях (3.13), является задачей частично целочисленного программирования. Частичную целочисленность задачи можно пояснить следующим образом. Прежде всего, заметим, что оптимальное решение линейной задачи можно записать в виде

(3.16)

x_опт = y₁ + y₂ +... + y_k0, k0 ≤ p,

где y₁ = h₁,..., y_k0–1 = h_k0–1, 0 < y_k < h_k, а все y_k для k > k₀ равны нулю. Здесь по существу намечена некоторая процедура поиска оптимального решения. В начале у₁ увеличивается до своего макси-мального значения. Если экстремум не достигнут, то, зафиксировав у₁ на максимальном значении, увеличивают у₂ от нулевого значения у₂ = 0 до максимального и т.д., пока не дойдут до у_k0. Если у_k0 взять максимальной, то нарушится соотношение (3.16). Необходимо эту переменную уменьшить до значения, удовлетворяющего соотношению (3.16). Остальные у_k (k > k₀) следует положить равными нулю, что является следствием выпуклости функции цели, которая обусловливает соотношения (3.15). В соответствии с этим условием нецелесообразно брать переменную у_k+1, отличную от нуля, пока у_k не достигла своего максимального значения. Формально последнее утверждение может быть записано с помощью следующих логических соотношений, носящих альтернативный характер:

(3.17)

<< или у_k – h_k = 0, или у_k+1 = 0>>.

Это условие в рассмотренной выше задаче минимизации (3.14) при условиях (3.13) не является дополнительным и автоматически выполняется при соблюдении условий (3.13).

Рассмотрим теперь невыпуклую функцию F(х) (рис. 3.10). Опять заменим исходную функцию цели приближенно кусочно-линейной функцией в соответствии с формулой (3.14). При этом не соблюдается условие монотонности коэффициентов c_k [см. формулу (3.15)]. Можно попытаться довести до верхней границы вначале значение у_k, соответствующее наименьшему c_k, затем значение y_k, соответствующее следующему по величине c_i, и т.д., однако при этом отрезки Δх, из которых комплектуется оптимальное значение х, получаются несвязными. Для обеспечения их связности необходимо условие (3.17) ввести как обязательное, так как оно в данном случае автоматически не выполняется. Сведем его к целочисленной программе. Для этого воспользуемся дополнительными переменными

(3.18)

z_k = 0 или 1, k = 1, 2,..., p.

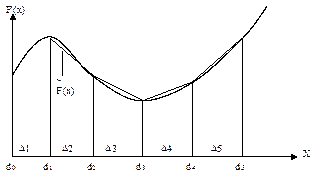
Рис 3.10. К методу сведения задач невыпуклого программирования
к задачам целочисленного программирования

Тогда условие (3.17) можно заменить соотношениями:

y_k ³ h_kz_k;

(3.19)

y_k+1 ≤ h_k+1z_k;

k = 1, 2,..., p-1.

Нетрудно убедиться, что z_k = 1 соответствует достижению у_k своей верхней границы, так как первое соотношение (3.19) превращается в y_k ³ h_k, т.е. y_k = h_k (переменная y_k по условию (3.13) не может быть больше h_k). Значение z_k соответствует условию у_k < h_k, так как второе соотношение (3.19) превращается в y_k+1 ≤ 0, которое в силу (3.13) означает, что у_k+1 = 0. Далее, замечая, что ограничения, наложенные сверху на у_k в соотношениях (3.13), уже содержатся в формулах (3.19), кроме ограничения на у₁, можно заменить ограничения (3.13) и (3.19) на следующие:

(3.20)

y_k ³ 0, k = 1, 2,..., p;

y₁ ≤ h₁;

(3.21)

y_k ³ h_k z_k;

y_k+1 ≤ h_kz_k;

k = 1, 2,..., p-1.

В итоге исходная задача невыпуклого программирования свелась к задаче целочисленного программирования:

F~(х) = c₀ + c₁y₁ + c₂y₂ +...+ c_py_p = min;

y_k ³ 0;

x = y₁ + y₂ +...+ y_p;

(3.22)

z = 0 или 1;

y₁ ≤ h₁;

y_k ³ h_kz_k;

y_k+1 ≤ h_kz_k;

k = 1, 2,..., p.

Кроме того, если в исходной нелинейной программе имеют место ограничения

φ_i(x) ≤ 0, i = 1, 2,..., m,

их следует добавить к ограничениям (3.22).

Приведенный выше способ сведения невыпуклой нелинейной программы к частично целочисленной программе реализуется за счет введения большого числа дополнительных переменных и ограничений.