Целочисленное программирование

Задача на условный экстремум

Задача на абсолютный экстремум

Классические методы определения экстремумов функции

Напомним, что если непрерывная функция n переменных х = (х₁,...,х_n) F(х) имеет в точке х _опт максимум, то существует ε > 0 такое, что для всех х из ε -окрестности точки х _опт

F(x) ≤ F(х _опт).

Выберем два вида приращения х_j вдоль j-й координаты:

Δх_j = х_j – х_jопт > 0;

Δх_j = х_j – х_jопт <0.

Тогда:

[F(х_j) – F(х_jопт)]/Δх_j ≤ 0 при Δх_j > 0;

[F(х_j) – F(х_jопт)]/Δх_j ³ 0 при Δх_j <0.

(3.5)

Переходя в этих соотношениях к пределу при х_j → 0, получаем:

¶ F(х_jопт)/ ¶ х_j ≤ 0; ¶ F(х_jопт)]/ ¶ х_j ³ 0.

Из этих соотношений следует (условия Ферма), что

(3.6)

¶ F(х_jопт)/ ¶ х_j = ¶ F(х _опт)/ ¶ х_j = 0; j = 1, 2,..., n.

Аналогичное соотношение можно получить для случая минимума функции. Таким образом, доказана необходимость условий (3.6) для достижения в точке х _опт максимума или минимума функции F(х), т.е. если имеется экстремум, то условия (3.6) удовлетворяются. Но равенство нулю всех производных в точке х _опт еще не обеспечивает существования в ней экстремума, т.е. условия (3.6) не являются достаточными. Геометрически это означает, что в случае нулевой производной от функции одной переменной может иметь место точка перегиба, а не максимум (или минимум), а в случае функции двух переменных – седловая точка, а не экстремум и т.д. Поэтому точки х _опт, в которых выполняются соотношения (3.6), называются стационарными.

Заметим, что условие (3.6) удалось получить благодаря возможности придавать переменной х приращения двух знаков, откуда и возникли два неравенства (3.5). Если допустимая область значений х ограничена неотрицательными значениями х ³ 0, то внутри области, где х > 0, справедливость условия (3.6) сохраняется, так как там допустимы приращения обоих знаков. На границе области х ³ 0, где х = 0, допускается только положительное приращение Δх > 0, можно говорить только об односторонней производной, и из (3.6) следует следующее необходимое условие максимума:

¶ F(х _опт)/ ¶ х_j ≤ 0.

Необходимое условие минимума на границе области х_j = 0 запишется в виде

¶ F(х _опт)]/ ¶ х_j ³ 0.

При определении условного экстремума функции, когда требуется определить максимум (или минимум) функции F(х) при ограничивающих условиях

φ_i(х) = b_i, i = 1,..., m,

т.е.

F(x) = max;

φ_i(х) = b_i,

используется также метод множителей Лагранжа, который, так же как в случае классического вариационного исчисления (см. юниту 1), заключается во введении функции Лагранжа

(3.7)

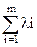Ф = F(x) + [b_i – φ_i(х)],

где 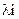– неопределенные множители Лагранжа.

Полагая, что функция является частным случаем функционала, получаем, что необходимые условия экстремума находятся прямым дифференцированием соотношения (3.7) и записываются в виде

(3.8)

¶ Ф/ ¶ x_j = ¶ F/ ¶ x_j + ∑λ_i(¶ φ_i/ ¶ х_j) = 0, j = 1,..., n;

(3.9)

¶ Ф/ ¶ λ_i = b_i – φ_i(х) = 0, i = 1,..., m.

Если ввести в рассмотрение векторы

λ = (λ₁,..., λ_m);

φ = (φ₁,..., φ_m);

b = (b₁,..., b_m);

gradf(x) = { ¶ f/ ¶ x₁, ¶ f/ ¶ x₂,..., ¶ f/ ¶ x_n},

соотношения (3.8) и (3.9) перепишутся как условия Лагранжа:

gradФ = gradF – λgradφ = 0;

b – φ = 0,

где равенство нулю векторов понимается покомпонентно.

В случае n = 2 и m = 1 геометрическая задача об отыскании условного экстремума сводится к отысканию точки касания А кривой φ = b к одной из кривых постоянного уровня F = const.