Примеры вычисления силовых функций однородного поля силы тяжести и линейной силы упругости

Однородное поле силы тяжести

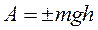
Рассмотрим материальную точку массой m, находящуюся в однородном поле силы тяжести. Направим ось Oz вертикально вверх, а оси Ox и Oy произвольно в горизонтальной плоскости.

Проекции силы тяжести 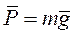на оси координат будут равны

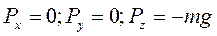
Элементарная работа силы тяжести

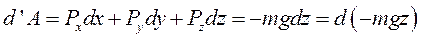
Так как элементарная работа силы тяжести является полным дифференциалом и 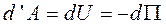, то, интегрируя, находим

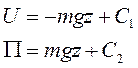(I)

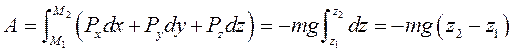
Где А – работа силы тяжести материальной точки массой m на перемещении 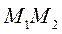. (I) можно представить в виде

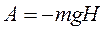
Где 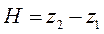- высота подъема точки.

Если точка 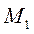расположена выше 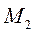, т.е. опускается, то работа положительная, иначе – отрицательная.

Поле линейной силы упругости.

Лиин. сила упр. подчиняется закону Гука

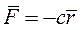
Элементарная работа этой силы:

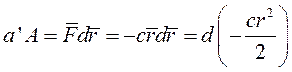
так как 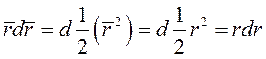. Интегрируем

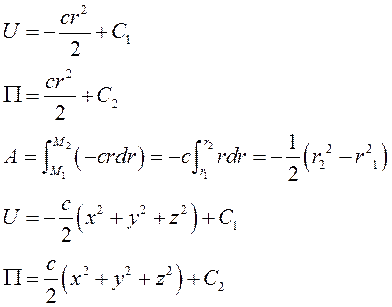
Таким образом, силовая функция и потенциальная энергия линейной силы упругости является квадратичной формой координат точки М, отсчитываемых от положения равновесия.

Работа силы упругости не зависит от траектории. При перемещении точки из положения равновесия работа силы упругости отрицательна

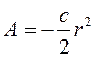
Поверхностями уровня линейной упругой силы будут концентрические сферы с центром в начале координат, а силовыми линиями – прямые, проходящие через начало координат, т.к. из

следует