2014-02-09
464
Данные измерения производятся для установления взаимосвязи между определяемыми параметрами и параметрами, которые мы находим с помощью прямых измерений.
Имеем: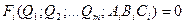 
, где Qi – определяемые нами параметры, заданные функцией Fi,
А, В и С – измеряемые физические величины.
После их подстановки имеем: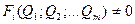 
Это было бы верно, если измеряемые значения Аi, Bi, Ci не содержали бы погрешностей, поэтому данное равенство не выполняется. Переводится оно в равенство за счет ввода дополнительного слагаемого, которое учитывает погрешности измерения. Это дополнительное слагаемое Vi называется невязкой. Задача обработки результата измерения в этом случае состоит в том, чтобы найти такие оценки параметра Q, чтобы сумма квадратов невязок была бы минимальной, то есть уравнение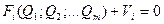 
удовлетворяло условию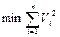 
Требование минимизации можно записать в виде: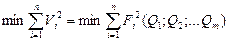 
Этот подход определения параметров уравнения связи носит название метода наименьших квадратов. Функция нескольких переменных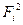 
достигает минимума в точке, где все ее частные производные равны 0. Отсюда получаем систему уравнений, позволяющую определить все интересующие нас параметры (Q1; Q2; … Qm).
|
|
|
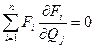, где j = 1, 2, 3 … m (m – число определяемых параметров), n – число измерений.
При найденном уравнении связи погрешность измерения далее, определяется как для косвенного измерения.
