Здесь рассматривают три случая:
1) Выполняется измерение с однократным наблюдением. В этом случае погрешность измерения полностью определяется классом точности используемого средства измерения. Результат измерения записывают в виде: 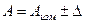 ,
,
где значение погрешности определяется классом точности используемого средства измерения.
2) Имеем небольшую выборку, число измерений не превышает 15 и второе – неизвестны систематические погрешности. При данных исходных данных, при обработки результатов прямых измерений ограничиваются двумя действиями:
1.определяют средние арифметические значения, которые и принимают за результат измерения: 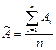
2.определяют значение среднеквадратического отклонения результата измерения: 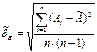
Результат записывается в виде: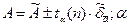
Если доверительная вероятность не дается, то результат записывают в следующей форме: 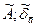
1) Число измерений больше 15 и значения систематических погрешностей определены. В этом случае производится полная обработка результатов прямых измерений:
1. Исключаем известные систематические погрешности из результатов измерений;
2. Определяем среднее арифметическое значение исправленных результатов измерений, которые принимаем за результат измерения: 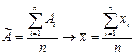 ;
;
3. Определяем СКО результата отдельного наблюдения 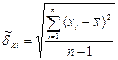 , где n – число наблюдений;
, где n – число наблюдений;
4. Определяем СКО результата измерения 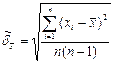 ;
;
5. Проверяем гипотезу о том, что результаты наблюдений принадлежат нормальному распределению (ГОСТ 11.006-74)
6. Определяем доверительные границы случайной составляющей погрешности измерения: 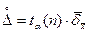 ,
,
где tα(n) – коэффициент Стьюдента, который определяется по таблице
7. Определяем границу неисключенной систематической погрешности j-ого результата наблюдения 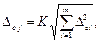
где 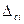 - составляющая основной погрешности средства измерения, К=1,1 для α=0,95
- составляющая основной погрешности средства измерения, К=1,1 для α=0,95
8. Определяем границу неисключенной систематической погрешности результата измерения 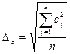
9. Определяем суммарную погрешность результата измерения:
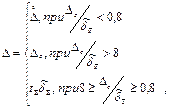 где
где 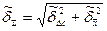
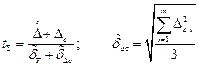
10. Результат измерения записывается в виде: 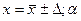
 2014-02-09
2014-02-09 1123
1123
