В поле напряжений вокруг краевой дислокации в точке с координатами х и у касательное напряжение в плоскости, параллельной плоскости скольжения:
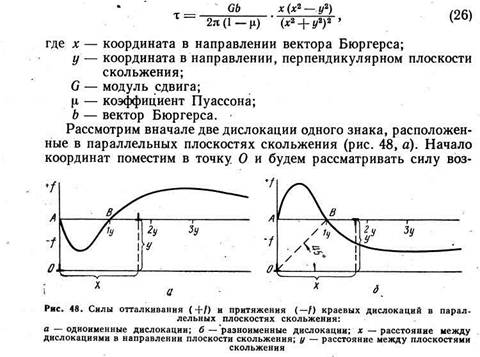
действия первой дислокации в точке O на вторую дислокацию, имеющую координаты х, у в параллельной плоскости скольжения. Учитывая, что сила, действующая на единицу длины второй дислокации, f = bτ, а также выражение (26) для τ, можно записать для силы взаимодействия параллельных краевых дислокаций одного знака:
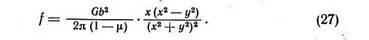
Таким образом, на рис. 48, а совмещены две схемы: одна показывает расположение одноименных краевых дислокаций в параллельных плоскостях скольжения, находящихся на расстоянии у одна от другой, а другая — зависимость силы взаимодействия этих дислокаций (f) от расстояния между ними в направлении скольжения (х). За единицу длины в направлении х принята величина у. В точке В х=у и f = 0 [рис. 48, а и формула (27)]. Правее точки В х > у и f > 0, т. е. одноименные дислокации взаимно отталкиваются. Левее точки В х < у и f < 0, т. е. одноименные краевые дислокации на относительно близких расстояниях взаимно притягиваются. Это притяжение — результат низкой симметрии поля напряжений вокруг краевой дислокации, результат внецентренного взаимодействия. Сила взаимодействия одноименных дислокаций равна нулю при х = 0 (в точке А) и при х = у (в точке В). Но в точке В равновесие неустойчиво, так как небольшие отклонения от нее вправо или влево приводят к возникновению силы, стремящейся удалить дислокацию от точки В. В точке А равновесие устойчиво: небольшие отклонения от точки А приводят к возникновению силы, стремящейся вернуть дислокацию в эту точку (левее точки А на рис. 48, а должна быть картина, симметричная той, что изображена правее этой точки). Таким образом, краевые дислокации одного знака, расположенные одна над другой, — механически устойчивая конфигурация.
Причину устойчивости такой конфигурации помогает понять следующая модель (рис. 49). В трех кристаллических полосах имеется по одной положительной дислокации. В верхней половине каждой полосы существует, следовательно, лишняя плоскость (экстраплоскость), которая, как клин, изгибает полосу (см. также рис. 22). Соединив полосы в одно целое, получаем кристалл с тремя дислокациями. Совершенно очевидно, что чем точнее совпадают места изгиба полос, тем меньше потребуется энергии для их соединения. Когда много одноименных дислокаций располагается одна под другой, такую устойчивую конфигурацию называют дислокационной стенкой.
Если одноименные дислокации находятся в одной плоскости скольжения, т. е. у = 0, то формула для силы их взаимодействия приобретает следующий вид:

Следовательно, между одноименными дислокациями, находящимися в одной плоскости скольжения, действует только сила взаимного отталкивания, обратно пропорциональная расстоянию между ними. Отсутствие взаимного притяжения в этом случае легко понять, так как при сближении двух экстраплоскостей чрезвычайно сильно искажается решетка, возрастает энергия.
Перейдем к рассмотрению взаимодействия разноименных краевых дислокаций в параллельных плоскостях скольжения, (рис. 48, б). Сила воздействия дислокации, помещенной в точке О, на дислокацию противоположного знака с координатами х, у определяется следующей формулой:
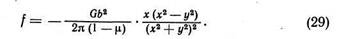
Это выражение отличается от рассмотренного ранее для силы взаимодействия одноименных дислокаций только знаком минус. При х > у f < 0, т. е. разноименные дислокации взаимно притягиваются. При х<у f >0, т. е. они взаимно отталкиваются. При х = 0 и х = у f = 0. В точке А равновесие неустойчиво, так как небольшое отклонение от этой точки вызывает появление силы, стремящейся удалить одну дислокацию от другой. В точке В (х = у) равновесие устойчиво: отклонение вправо и влево от точки В вызывает появление силы, стремящейся возвратить дислокацию в эту точку. Таким образом, линия, соединяющая разноименные дислокации, образующие устойчивую конфигурацию, находится под углом 45° к плоскости скольжения. Если разноименные краевые дислокации находятся в одной плоскости скольжения (у = 0), то между ними действует только сила взаимного притяжения, обратно пропорциональная расстоянию между дислокациями:
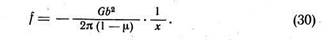
Когда сближающиеся в одной плоскости скольжения (рис. 50, а) дислокации разного знака подходят вплотную одна к другой, они взаимно уничтожаются. Такую аннигиляцию легко себе представить: две экстраплоскости сливаются в единую полную атомную плоскость.

Если же разноименные дислокации находятся не в одной плоскости скольжения, а в соседних плоскостях, разделенных одним межатомным расстоянием (рис. 50, б и в), то после их сближения образуется цепочка вакансий (б) между кромками экстраплоскостей или цепочка межузельных атомов (в), оказавшаяся «лишней» при слиянии экстраплоскостей в одну полную плоскость. При увеличении расстояния между плоскостями скольжения притяжение разноименных дислокаций переходит в рассмотренное выше взаимное отталкивание на коротких расстояниях вдоль плоскости скольжения.
 2014-02-09
2014-02-09 1455
1455
