Одинаков вдоль всей линии дислокации, т. е. является инвариантом дислокации. Это следует, например, из того, что при смещении контура Бюргерса вдоль линии дислокации он все время будет оставаться эквивалентным исходному контуру (при условии, что он всеми своими точками не выходит из совершенной области решетки, т. е. не пересекает другие несовершенства). Кроме того, вектор сдвига, создающего, например, криволинейную смешанную дислокацию (см. рис. 37), имеет одну величину и одно направление для всего кристалла.
У дефектов недислокационного типа равен нулю. Если построить контур Бюргерса вокруг любого точечного дефекта или линейного дефекта недислокационного типа (вокруг цепочки атомов или вакансий), то соответствующий контур в идеальном кристалле окажется замкнутым.
Нормален к линии краевой дислокации и параллелен линии винтовой дислокации. Вдоль линии смешанной дислокации угол между ней и вектором Бюргерса в разных точках имеет разную величину (см. рис. 37).
Из инвариантности вектора Бюргерса вытекает важное следствие: дислокация не может обрываться внутри кристалла. Допустив противное, продвинем контур Бюргерса за предполагаемую точку обрыва дислокации. Контур останется неизменным, так как все время находится в области с совершенной решеткой.
|
|
|
Но если ему соответствует прежний вектор Бюргерса, отличный от нуля, это значит, что внутри контура Бюргерса все время присутствует дислокация, т. е. обрыв ее внутри кристалла невозможен. Дислокация может обрываться только на границе кристалла. Внутри кристалла дислокации могут образовывать замкнутые петли с одинаковым вектором Бюргерса вдоль всей петли или встречаться с другими дислокациями, образовывая узлы (точки встречи).
То, что дислокация не обрывается внутри кристалла, можно доказать, как уже упоминалось в § 14, следующим весьма наглядным путем. Дислокация является границей зоны сдвига (см. § 9), которая должна быть замкнутой линией (часть этой линии может проходить по поверхности кристалла, как, например, на рис. 21).
Из § 10, 13 и 14 следует, что вектор Бюргерса и линия дислокации однозначно определяют возможную плоскость (поверхность) скольжения.
Поскольку вектор Бюргерса — столь важная количественная характеристика дислокации, необходимо уметь обозначать его так, чтобы запись его отражала направление и величину вектора.
Если вектор b по трем координатным осям х, у и z имеет составляющие bx, by и bz, то это записывается так: b = lbxbybz].
Величину вектора Бюргерса или, как часто говорят, его мощность легко определить:
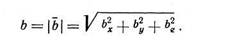
За направления осей x, у и z обычно принимают кристаллографические направления ребер элементарной ячейки данной решетки. В случае кубической решетки составляющие по осям b х, bу и b z можно выразить через период элементарной ячейки а. Этот период войдет в общий наибольший делитель па, где п — некоторое число. Тогда
|
|
|

Здесь u, v и w — целые числа, a luvw] является символом кристаллографического направления вектора Бюргерса. 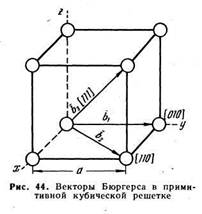

Дислокация повышает энергию кристалла. Она — центр поля внутренних напряжений, убывающих с увеличением расстояния от дислокации. В ядре дислокации смещения атомов настолько велики, что рассчитать энергию здесь с помощью методов теории упругости не удается. За пределами ядра дислокации деформации описываются линейными уравнениями теории упругости, и поле напряжений и соответствующую энергию легко вычислить.
Для оценки энергии винтовой дислокации введем допущение, что в процессе ее образования кристалл ведет себя как упругое изотропное твердое тело. Возьмем такой совершенный кристалл, сделаем в нем несквозной надрез и сдвинем две части этого кристалла одну относительно другой по плоскости надреза на величину b так, как это уже рассматривалось на рис. 29. Такой сдвиг происходит под действием касательных сил и соответствующих напряжений в плоскости надреза. Работа, совершенная этими силами для создания смещения b равна энергии винтовой дислокации
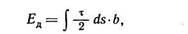
где τ — касательное напряжение, вызывающее сдвиг на величину b.
В период сдвига напряжение линейно возрастает от 0 до τ. Поэтому при расчете энергии сдвига необходимо брать среднюю за весь период сдвига величину
касательного напряжения, равного τ/2.
Для малых сдвиговых деформации справедлив закон Гука:
τ = Gb/2πr (G — модуль сдвига). Это касательное напряжение действует на площадке ds = ldr. Тогда
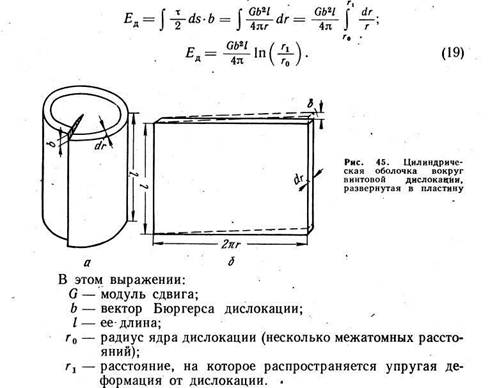
. Для наиболее типичных значений r1 и r0 выражение (19) можно записать в очень удобном для многих расчетов виде:
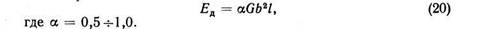
Вполне естественно, что энергия дислокации зависит от вектора Бюргерса, характеризующего степень искаженности решетки, и от модуля сдвига, являющегося характеристикой сил межатомной связи. Чем больше G, тем сильнее межатомные силы сопротивляются смещениям атомов, т. е. больше накапливается упругая энергия искажений решетки.
Разные оценки показывают, что потенциальная энергия ядра дислокации по порядку величины не превышает одну десятую энергии, связанной с упругой деформацией за пределами ядра дислокации. Вследствие неопределенности расчетов общую энергию дислокации считают равной αGb2l. Для разных твердых тел энергия винтовых дислокаций обычно находится в пределах от 3 до 10 эВ в расчете на одно межатомное расстояние вдоль линии дислокации.
Увеличение длины дислокации приводит к росту ее упругой энергии. Поэтому линия дислокации ведет себя как упругая нить, всегда стремящаяся выпрямиться, чтобы сократить свою длину. Энергию дислокации, приходящуюся на единицу ее длины, называют линейным натяжением дислокации:

Сила линейного натяжения направлена вдоль линии дислокации.
Энергия дислокации, приходящаяся на единицу ее длины, не является константой. Она зависит от типа дислокации, ее расстояния от соседних дислокаций и от поверхности кристалла и других факторов.
Выше рассматривалась энергия неподвижной дислокации. Поля напряжений движущейся и неподвижной дислокации различны, что объясняется возникновением инерциальных сил от движения элементов тела, вызванного движением дислокации.
Уравнения движения дислокации сходны с уравнениями движения частицы, приводимыми в теории относительности. Здесь скорость звука в данном материале является такой же предельной скоростью, как скорость света в теории Эйнштейна. С приближением скорости дислокации v к скорости звука в кристалле с энергия дислокации бесконечно возрастает. Энергия винтовой дислокации
|
|
|
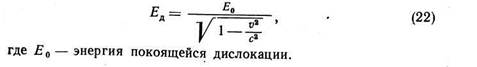
 2014-02-09
2014-02-09 2927
2927
