2014-02-09
2261
КОНТРОЛЬНЫЕ ВОПРОСЫ 9
1. Сформулируйте задачу выбора оптимальной производственной программы, когда прибыль от реализации единицы продукции, запасы сырья и материалов являются случайными величинами.
2. Можно ли максимизировать суммарную прибыль от реализации продукции в стохастической модели и почему?
3. Какие детерминированные характеристики должны быть известны для решения стохастической задачи?
4. Приведите ММ двухкритериальной стохастической задачи при случайных значениях прибыли.
5. Приведите ММ двухкритериальной стохастической задачи при случайных значениях объема ресурсов.
6. Приведите стохастическую однокритериальную модель оптимальной производственной программы при случайной доступности ресурсов.
7. Как изменятся ограничения в стохастических задачах ПР?
8. Сформулируйте задачу выбора оптимальной цены в торговом центре, обеспечивающей максимум математического ожидания величины дохода.
9. Запишите ММ стохастической модели выбора оптимальной цены в торговом центре.
|
|
|
|
В приведенных выше задачах использовалось несколько критериев оптимальности решений, характерных именно для задач ТПР.
Отметим, что если в однокритериальных задачах возможно получение единственного оптимального решения (Рис. 6.1 а), то в многокритериальных ЗПР такая возможность отсутствует (Рис. 6.1 б).
 |
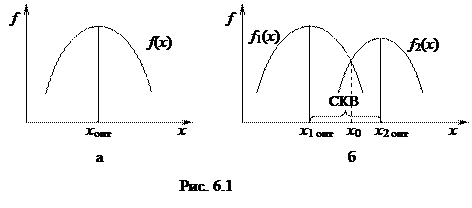В многокритериальных задачах возможно получение совокупности компромиссных вариантов (СКВ) решений на интервале [ х 1 опт, х 2 опт].
Здесь х 1 опт, х 2 опт соответственно точки максимума функций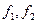 
. Из рисунка 6.1 б видно, что точка, доставляющая максимум обеим функциям одновременно, отсутствует.
Для решения многокритериальных задач обычно используют два подхода:
1. Сведение многокритериальных задач к однокритериальным путем «свертки» критериев (в данном случае можно получить единственное оптимальное решение x 0).
2. Построение множества эффективных решений (оптимальных по Парето).
Рассмотрим наиболее распространенную на практике двухкритериальную ММ, которая в общем виде записывается как:
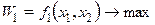; (6.1)
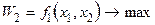; (6.2)
, 
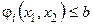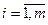; (6.3)
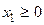; х 2 ≥ 0. (6.4)
Ограничения (6.3), (6.4) определяют область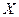 
допустимых решений задачи (6.1) - (6.4), то есть замкнутую область на плоскости 
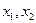(рис. 6.2).
Выберем в этом множестве точку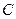 
с координатами 
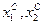, подставим координаты этой точки в целевые функции (6.1) и (6.2) и получим значения 
.
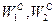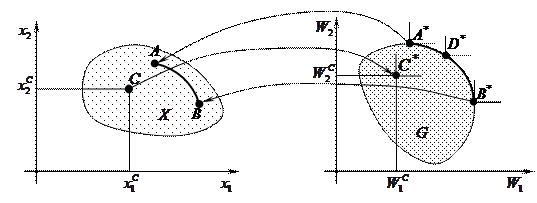
Рис. 6.2
Введем в рассмотрение пространство значений критериев 
. В этом пространстве величины определяют некоторую точку 
(см. рис. 6.2). Перебирая все точки множества 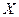, получим в пространстве критериев некоторое замкнутое множество 
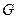, называемое множеством достижимости задачи (6.1) - (6.4). Таким образом, можно утверждать, что функции (6.1) и (6.2) проводят отображение множества 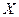в множество .
|
|
|
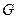Выделим в множестве 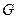четыре точки: 
.
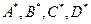Точка 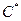является внутренней точкой множества 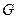, точка 
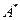порождается решением однокритериальной задачи вида (6.2) - (6.4). Решение этой задачи обозначим как 
, 
, 
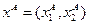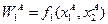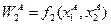. Точка 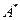является наиболее удаленной точкой множества 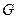по оси 
.
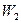Точка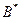 
получается из решения задачи (6.1), (6.3), (6.4). Эта точка является наиболее удаленной точкой множества 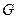по оси 
.
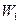Точка 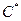является заведомо «плохой», так как в множестве 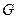можно найти более лучшую точку (например, D) такую, что 
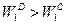и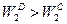 
.
Для точек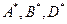 
более лучших точек в пространстве критериев 
не существует. Именно такие точки, для которых не существует точек более лучших, составляют множество точек оптимальных по Парето в пространстве критериев. В нашем случае такое множество составляют точки, лежащие на кривой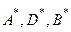 
.
Для выявления лучших (эффективных) точек множества 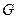используется правило ортанта (конуса) 
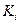с вершиной в точке 
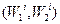. Уравнение этого конуса имеет вид:
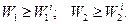
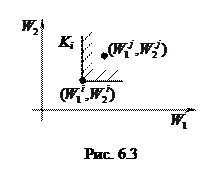Графически данный конус представлен на рис. 6.3.
Правило выделения эффективных точек: Если в конусе 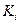лежит хотя бы одна точка 
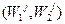из области достижимости, то она является более предпочтительной, чем точка 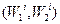. Все точки множества 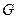, для которых соответствующие конусы являются пустыми, составляют множество паретооптимальных решений в пространстве критериев.
Строя обратное отображение этого множества в пространство решений (в множество допустимых решений, задаваемое неравенствами (6.3), (6.4)), получаем множество оптимальных по Парето решений в пространстве решений. На рис. 6.2 эти точки лежат на кривой АВ.
Аналогичный подход рассматривается и для других видов двухкритериальных задач. В частности, уравнения конусов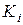 
для соответствующих задач примут вид:
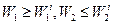для задачи 
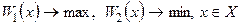; (6.5)
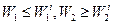для задачи 
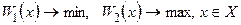; (6.6)
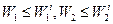для задачи 
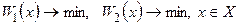; (6.7)
Пусть требуется решить задачу вида (6.1) - (6.4). Пусть критерий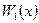 
является более важным для принятия решения, чем критерий 
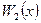. Заказчик оценил степени важности критериев с помощью двух чисел 
, 
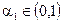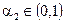таких, что 
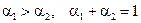. Построим на их основе функцию
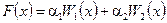, (6.8)
которая называется линейной сверткой критериев 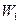и 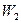. Тогда оптимальное решение 
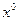задачи (6.1) - (6.4) получается как решение задачи вида:
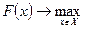. (6.9)
Задача (6.5) может быть сведена к задаче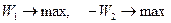 
(или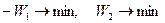 
). Свертка будет иметь вид:
.
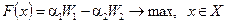Свертка для задачи (5.6):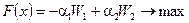 
.
Для задачи (6.7):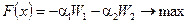 
или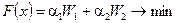 
.
Вводя обозначение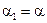 
, свертку (6.8) можно переписать как:
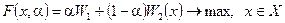. (6.10)
Здесь параметр свертки a должен удовлетворять условию
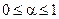. (6.11)
Решая задачу максимизации свертки при различных значениях a, удовлетворяющих условию (6.11), получаем множество оптимальных решений вида
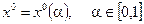. (6.12)
Эти решения называются оптимальными решениями по Парето в пространстве решений. Подставляя их в целевые функции, получаем
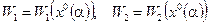. (6.13)
Эти выражения описывают на координатной плоскости 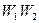некоторую кривую, которую называют оптимальным по Парето решением в пространстве критериев. На
рис. 6.2 – это кривая А * В *. Точка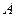 
* – наиболее удаленная по координате 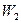. Эта точка получается, если в свертке (6.10) положить a = 0 и решить задачу вида: 
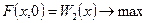; точка 
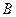* является наиболее удаленной точкой по координате 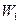. Ее координаты получаются при 
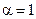из решения задачи оптимизации вида 
.
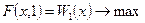Доказано, что если множество допустимых решений 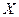выпукло и ограничено, а целевые функци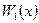и и 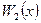являются унимодальными функциями (имеют один максимум или один минимум в области допустимых решений), то произвольная точка 
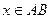получается при подстановке в решение (6.12) произвольного значения параметра a, удовлетворяющему условию (6.11).
Определим алгоритм решения задачи:
1) Разбиваем интервал (6.11) на точки: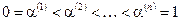 
.
2) Каждое значение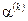 
, 
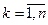подставляется в свертку (6.10) и решается однокритериальная задача 
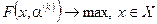. В результате получается решение вида (6.12) для 
.
|
|
|
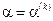3) Эти решения подставляются в целевые функции (6.13); строится кривая А * В *, то есть оптимальные по Парето решения в пространстве критериев 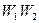. Эта кривая А * В * используется ЛПР для выбора из всего множества решений (6.12) единственного оптимального решения.
При движении по кривой из точки 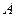* в 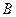* значение целевой функции 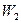будет ухудшаться (она уменьшается), а значение 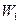будет улучшаться (она увеличивается).
ЛПР, исходя из неформальных соображений, должен выбрать некоторый компромисс – точку D *, значения критериев в которой его устраивают. Для данной точки D * устанавливается то значение a, при котором она была получена и с помощью выражения (6.12) находится единственное оптимальное решение.
