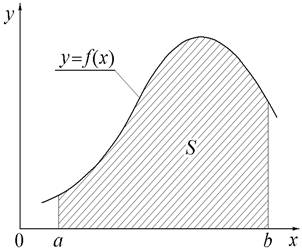
 Определенный интеграл в геометрическом смысле равен площади геометрической фигуры, ограниченной сверху и снизу кривой
Определенный интеграл в геометрическом смысле равен площади геометрической фигуры, ограниченной сверху и снизу кривой 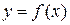 и осью абсцисс, а слева и справа – пределами интегрирования (см. рис.), т.е.
и осью абсцисс, а слева и справа – пределами интегрирования (см. рис.), т.е. 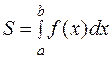 . Как видно из формулы и из рисунка 1.1, величина
. Как видно из формулы и из рисунка 1.1, величина 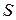 является числом со знаком. Если подынтегральная функция
является числом со знаком. Если подынтегральная функция 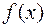 пересекает в пределах участка интегрирования ось абсцисс, то результат вычисления является разностью площадей над осью абсцисс и под ней
пересекает в пределах участка интегрирования ось абсцисс, то результат вычисления является разностью площадей над осью абсцисс и под ней
значение определенного интеграла можно вычислить с помощью следующих методов:
1.метод прямоугольников,
2. метод трапеций,
3. метод парабол (метод Симпсона).
Заданные точки разбивают весь отрезок интегрирования 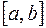 на равныеучастки
на равныеучастки 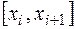
 2014-02-24
2014-02-24 359
359







