Введем соответствующее расстояние 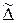 между данной непрерывной функцией f(х) и непрерывным аппроксимирующим обобщенным полиномом Q(x) (вообще говоря, более простой природы), так называемое среднее квадратичное отклонение.
между данной непрерывной функцией f(х) и непрерывным аппроксимирующим обобщенным полиномом Q(x) (вообще говоря, более простой природы), так называемое среднее квадратичное отклонение.
Определение. Под средним квадратичным отклонением функций f(х) и Q(x) на множестве точек X={x1, x2,..., хп} понимается число
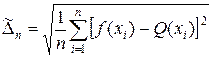 . (10.1)
. (10.1)
Если аппроксимация интегральная, то среднее квадратичное отклонение на отрезке [а, b] определяется формулой
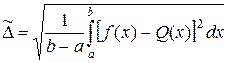 . (10.2)
. (10.2)
Формулу (10.2) можно рассматривать как предельный случай формулы (10.1) при n→∞. Действительно, выбирая на отрезке [а, b] систему равноотстоящих точек a=x1, x2,…,xn=b, где
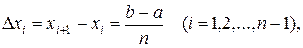
будем иметь
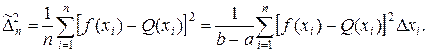
Отсюда при n→∞ получим
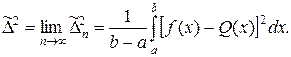
Если среднее квадратическое отклонение 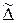 мало, то для «подавляющего большинства» значений аргумента x из отрезка [а, b] (т.е. в «среднем» на [а, b]) абсолютная величина
мало, то для «подавляющего большинства» значений аргумента x из отрезка [а, b] (т.е. в «среднем» на [а, b]) абсолютная величина 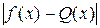 также мала при
также мала при 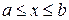 . Более точно, пусть
. Более точно, пусть 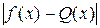 имеет на [а, b] конечное число экстремумов и α – заданное положительное число. Обозначим через
имеет на [а, b] конечное число экстремумов и α – заданное положительное число. Обозначим через 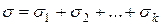 максимальную систему непересекающихся отрезков из [а, b] таких, что
максимальную систему непересекающихся отрезков из [а, b] таких, что
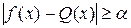
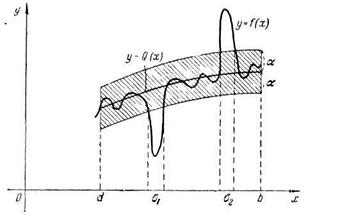
при 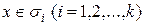 (рис. 6), и пусть ω – сумма длин этих отрезков. Если
(рис. 6), и пусть ω – сумма длин этих отрезков. Если 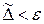 , то имеем
, то имеем
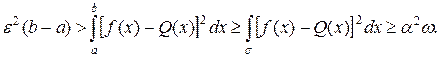
Отсюда
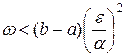
и, следовательно, ω – сколь угодно малое число, если ε достаточно мало. Таким образом, если 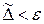 , где ε достаточно мало, то на отрезке [а, b], за исключением, быть может, множества точек σ, сколь угодно малой линейной меры ω, выполнено неравенство
, где ε достаточно мало, то на отрезке [а, b], за исключением, быть может, множества точек σ, сколь угодно малой линейной меры ω, выполнено неравенство
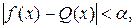
где α – произвольное заранее заданное положительное число.
Во многих случаях, например при обработке результатов наблюдений, квадратичное приближение является приемлемым, так как оно сглаживает отдельные локальные неправильности функции f(х) (возникшие, возможно, от ошибок наблюдений) и дает достаточно точное общее представление о протекании соответствующего процесса. Однако иногда для приближения ставят более жесткие условия, а именно требуется гарантировать, чтобы на всем отрезке [а, b] отклонение функций f(x) и Q(x) было меньше заданной величины. Поэтому введем другое расстояние между функциями, так называемое абсолютное отклонение.
|
рис. 6
Определение. Абсолютным отклонением на [а, b] обобщенного полинома Qm (x) от данной непрерывной функции f(х) называется число
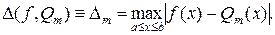 (10.3)
(10.3)
Если 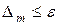 , то из формулы (10.3) следует
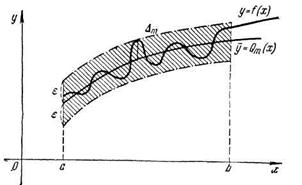
, то из формулы (10.3) следует 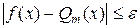 для всех точек х на отрезке [а, b] (рис. 7).
для всех точек х на отрезке [а, b] (рис. 7).
|
рис. 7
В этом случае говорят, что обобщенный полином Qm(x) на отрезке [a,b] равномерно приближает функцию f(х) с точностью до ε.
Для случая обычных полиномов
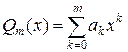
справедлива важная аппроксимационная теорема Вейерштрасса.
Теорема Вейерштрасса. Если функция f(х) непрерывна на отрезке [а,b], то, как бы мало ни было положительное число ε, найдется полином Qm (x) достаточно высокой степени т, абсолютное отклонение которого от данной функции f(x) на отрезке [а,b] меньше, чем ε, т. е. для всех точек 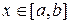 имеет место неравенство
имеет место неравенство
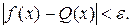
В частном случае, если функция f(x) аналитическая на отрезке [a,b], т. е. разлагается на этом отрезке в равномерно сходящийся степенной ряд (ряд Тейлора)
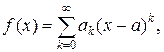
где
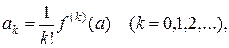
то за полином Qm(x) можно взять отрезок ряда Тейлора
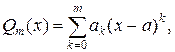
причем степень m подбирается в зависимости от заданной точности ε.
Пусть степень m полинома 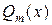 фиксирована и задача состоит в том, чтобы приблизить данную непрерывную функцию f(x) полиномом фиксированной степени m наилучшим образом на заданном множестве l. Это значит, что коэффициенты
фиксирована и задача состоит в том, чтобы приблизить данную непрерывную функцию f(x) полиномом фиксированной степени m наилучшим образом на заданном множестве l. Это значит, что коэффициенты 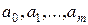 полинома
полинома
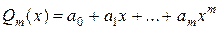 (10.4)
(10.4)
следует подобрать так, чтобы величина
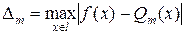 (10.5)
(10.5)
была минимальной.
Такой полином называют полиномом наилучшего приближения.
 2014-02-24
2014-02-24 1914
1914








