Метод Ньютона. Рассмотрим, вообще говоря, нелинейную систему уравнений
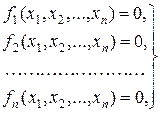 (9.1)
(9.1)
с действительными левыми частями.
Запишем короче систему (9.1). Совокупность аргументов х1, х2,…, хп можно рассматривать как n -мерный вектор
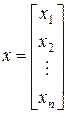 .
.
Аналогично совокупность функций f1, f 2,..., fn представляет собой также n -мерный вектор (вектор-функцию)
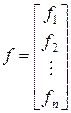 .
.
Поэтому система (9.1) кратко записывается так:
f(x) = 0. (9.2)
Для решения системы (9.2) будем пользоваться методом последовательных приближений.
Предположим, что найдено р -еприближение
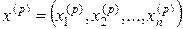
одного из изолированных корней х=(x1, х2,..., хп) векторного уравнения (9.2). Тогда точный корень уравнения (9.2) можно представить в виде
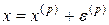 , (9.3)
, (9.3)
где 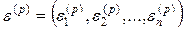 - поправка (погрешность корня).
- поправка (погрешность корня).
Подставляя выражение (9.3) в уравнение (9.2), будем иметь:
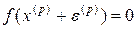 . (9.4)
. (9.4)
Предполагая, что функция f(x) непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x(p), разложим левую часть уравнения (9.4) по степеням малого вектора ε(p), ограничиваясь линейными членами,
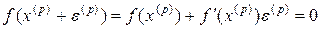 (9.5)
(9.5)
или, в развернутом виде,
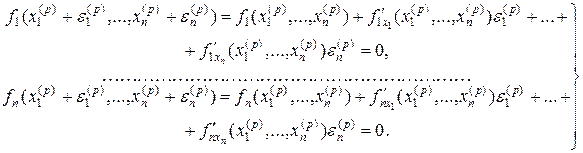 (9.6)
(9.6)
Из формул (9.5) и (9.6) вытекает, что под производной f ´(x) следует понимать матрицу Якоби системы функций f1, f2,…,fn относительно переменных x1, x2,…,xn, т.е.
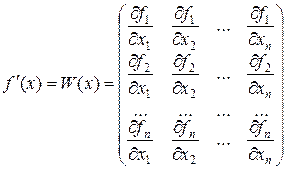 ,
,
или в краткой записи
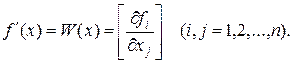
Система (9.6) представляет собой линейную систему относительно поправок 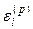 (i=1,2,…,n) с матрицей W(x), поэтому формула (9.5) может быть переписана в виде
(i=1,2,…,n) с матрицей W(x), поэтому формула (9.5) может быть переписана в виде
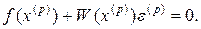
Отсюда, предполагая, что матрица 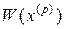 - неособенная, получим:
- неособенная, получим:
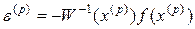 .
.
Следовательно,
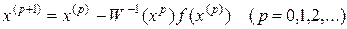 (9.7)
(9.7)
(метод Ньютона).
За нулевое приближение x(0) можно взять грубое значение искомого корня.
Метод итерации. Пусть дана система нелинейных уравнений специального вида
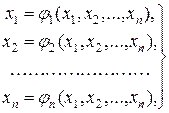 (9.8)
(9.8)
где функции 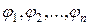 действительны, определены и непрерывны в некоторой окрестности ω изолированного решения
действительны, определены и непрерывны в некоторой окрестности ω изолированного решения 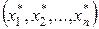 этой системы.
этой системы.
Введя в рассмотрение векторы
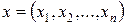 и
и 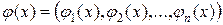 ,
,
систему (9.8) можно переписать более кратко:
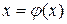 . (9.9)
. (9.9)
Для нахождения вектор-корня 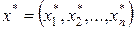 уравнения (9.9) часто удобно использовать метод итерации
уравнения (9.9) часто удобно использовать метод итерации
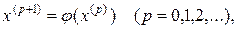 (9.10)
(9.10)
где начальное приближение 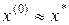 . Заметим, что если процесс итерации (9.10) сходится, то предельное значение
. Заметим, что если процесс итерации (9.10) сходится, то предельное значение
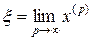 (9.11)
(9.11)
обязательно является корнем уравнения (9.9). Действительно, предполагая, что соотношение (9.11) выполнено, и переходя к пределу в равенстве (9.10) при р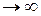 , в силу непрерывности функции φ(х) будем иметь:
, в силу непрерывности функции φ(х) будем иметь:
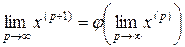 ,
,
т.е.
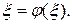
Таким образом, ξ есть корень векторного уравнения (9.9).
Если, сверх того, все приближения х(p) (р = 0, 1, 2,...) принадлежат области ω и х* — единственный корень системы (9.10) в ω, то, очевидно,
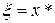 .
.
Метод итерации может быть применен также к общей системе
f(x)=0, (9.12)
где f(x) —вектор-функция, определенная и непрерывная в окрестности ω изолированного вектор-корня х*. Например, перепишем эту систему в следующем виде:
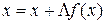 ,
,
где Λ — неособенная матрица. Введя обозначение
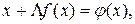 (9.13)
(9.13)
будем иметь
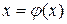 . (9.14)
. (9.14)
К последнему уравнению легко применяется обычный метод итерации (9.10).
Если функция f(x) имеет непрерывную производную f ´ (х) в ω, то из формулы (9.13) вытекает:
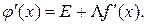
Процесс итерации для уравнения (9.14) быстро сходится, если 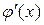 мала по норме. Учитывая эго обстоятельство, выбираем матрицу Λ так, чтобы
мала по норме. Учитывая эго обстоятельство, выбираем матрицу Λ так, чтобы
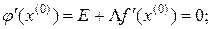
отсюда, если матрица 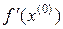 - неособенная, будем иметь:
- неособенная, будем иметь:
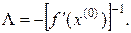
В случае, если 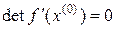 , то следует выбрать другое начальное приближение
, то следует выбрать другое начальное приближение 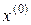 .
.
 2014-02-24
2014-02-24 1136
1136
