Конечные разности

Конечные разности различных порядков. Пусть

y = f(x) — заданная функция. Обозначим через Δ х =h фиксированную величину приращения аргумента (шаг). Тогда выражение

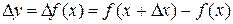(11.1)

называется первой конечной разностью функции у. Аналогично определяются конечные разности высших порядков

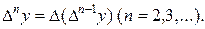
Например,

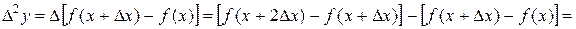
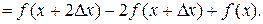
Пример 11.1. Построить конечные разности для функции Р(х) = х³, считая шаг Δ х= 1.

Решение. Имеем:

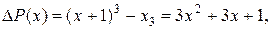
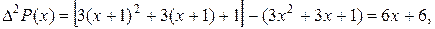
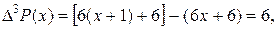
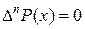при n >3.

Обратим внимание, что конечная разность третьего порядка функции Р(х) постоянна.

Вообще, справедливо утверждение: если

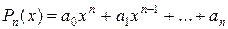
- полином n -ой степени, то 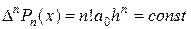, где .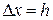

Действительно, имеем:

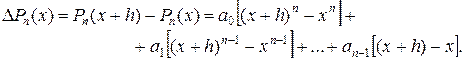
Раскрыв по биному Ньютона круглые скобки, легко убедиться, что 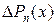представляет собой полином (n- 1)-ой степени:

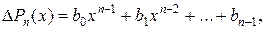
где

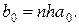
Рассуждая аналогично, приходим к выводу, что вторая разность 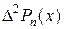есть полином (n -2)-ой степени:

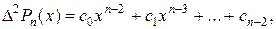
причем

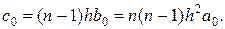
Проводя последовательно аналогичные рассуждения, мы в конце концов установим, что

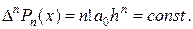
Как следствие получаем

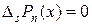при s>n.

Символ Δ (дельта) можно рассматривать как оператор, ставящий в соответствие функции у = f (х) функцию Δу =f(х+Δx)—f(х) (Δ х постоянно). Легко проверить основные свойства оператора Δ:

1)

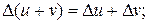
2) 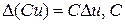- постоянная;

3) 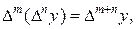где m и n – целые неотрицательные числа, причем по определению полагают .

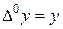Из формулы (11.1) имеем:

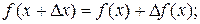
отсюда, рассматривая Δ как символический множитель, получим:

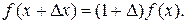(11.2)

Последовательно применяя это соотношение n раз, будем иметь:

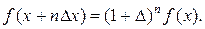(11.3)

Воспользовавшись формулой бинома Ньютона, окончательно выводим:

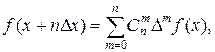(11.4)

где

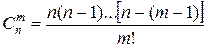
- число сочетаний из n элементов по m.

Таким образом, с помощью формулы (11.4) последовательные значения функции f(x) выражаются через ее конечные разности различных порядков.

Воспользовавшись тождеством

Δ=(1+Δ)-1 (11.5)

и применяя бином Ньютона, получаем:

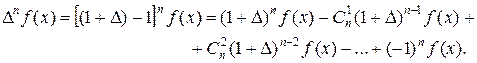
Отсюда в силу формулы (11.3) будем иметь:

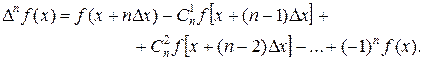(11.6)

Формула (11.6) дает выражение конечной разности n -го порядка функции f(х) через последовательные значения этой функции.

Пусть функция f(х) имеет непрерывную производную f⁽ⁿ⁾(х) на отрезке (х,x+nx). Тогда справедлива важная формула

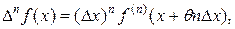(11.7)

где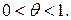

Формулу (11.7) проще всего доказать, используя метод математической индукции.

В самом деле, при п = 1 мы получаем теорему Лагранжа о конечном приращении функции и, следовательно, формула (11.7) верна. Пусть теперь при k < n имеем:

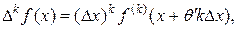
где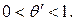

Тогда

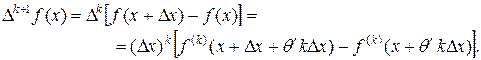
Применяя теорему Лагранжа к получившемуся приращению производной f^(k) (х), будем иметь:

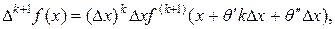
где 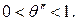Полагая

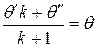, (11.8)

окончательно получим:

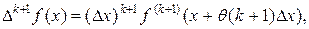
где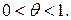

Таким образом, установлен переход oт k к k+1 и, следовательно формула (11.7) доказана.

Из формулы (11.7) имеем:

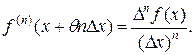
Отсюда, переходя к пределу при Δх→0 и предполагая, что производная f⁽ⁿ⁾(x) непрерывна, получим:

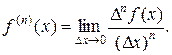(11.9)

Следовательно, при малых Δ х справедлива приближенная формула

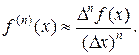(11.10)

Таблица разностей. Часто приходится рассматривать функции у=f(х), заданные табличными значениями y_i = f(x_i) для системы равноотстоящих точек х_i (i=0, 1, 2,...), где

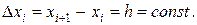
Конечные разности последовательности у_i естественно определяются соотношениями

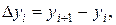
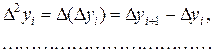
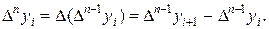
Из первого равенства имеем:

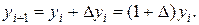
Отсюда последовательно выводим:

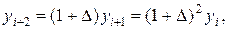
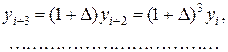
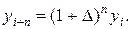
Использовав формулу бинома Ньютона, получим:

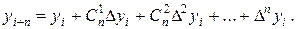
Обратно, имеем:

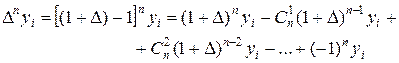
или

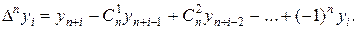
Например,

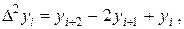
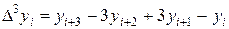
и т.д. Заметим, что для вычисления n -ой разности 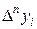нужно знать n+1 членов 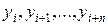данной последовательности.

Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной таблицы разностей (таблица 11.1) или диагональной таблицы разности (таблица 11.2).

Горизонтальная таблица разностей

x	y	Δ y	Δ 2y	Δ 3y
x0 x1 x2 …	y0 y1 y2 …	Δ y0 Δ y1 Δ y2 …	Δ 2y0 Δ 2y1 Δ 2y2 …	Δ 3y0 Δ 3y1 Δ 3y2 …