Теоретическая часть. Интерполирование функций

Интерполирование функций.

Цель работы: изучение методов интерполирования функций с помощью алгебраических многочленов.

Постановка задачи. Интерполировать функцию f(x) на отрезке [a,b] полиномами Лагранжа. Исследовать точность и устойчивость интерполяции, а также влияние на точность и устойчивость особых точек функции f(x).

Пусть на отрезке 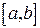даны n+1 различных значений аргумента: 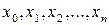и известны для функции y=f(x) соответствующие значения: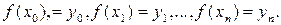

Построим полином 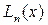степени не выше n, имеющий в заданных узлах 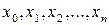те же значения, что и функция f(x), т.е. такой, что 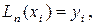i=0,1,...,n.

Построим сначала фундаментальный полином такой, что

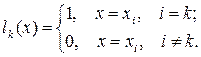
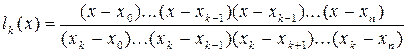, (3.1)

Введем функцию 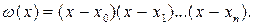Тогда 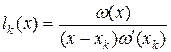. Это справедливо, так как

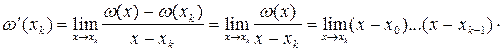
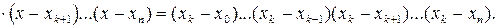
Интерполяционный полином Лагранжа будет иметь следующий вид

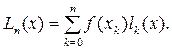(3.2)

Действительно, легко проверить, что полином (3.2) имеет степень n, и его значения совпадают со значениями интерполируемой функции в узлах интерполяции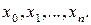

Укажем схему, облегчающую вычисление коэффициентов при 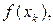k=0,1,...n, в формуле Лагранжа (3.2), так называемых лагранжевых коэффициентов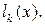

Для вычисления лагранжевых коэффициентов (3.1) можно использовать следующую схему. Запишем таблицу разностей следующим образом:

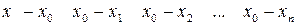
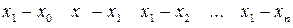
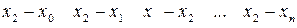(3.3)

..................................

..................................

.

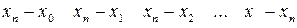Обозначим произведение элементов первой строки через 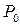, второй - через 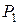и т.д., n-ной - через 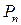. Произведение элементов главной диагонали, как нетрудно видеть, будет w(x). Отсюда следует, что

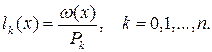(3.4)

Следовательно,

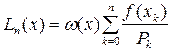. (3.5)

Погрешность интерполяции многочленом Лагранжа (3.2) определяется формулой

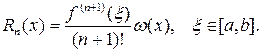(3.6)

При построении интерполяционного полинома большое значение имеет выбор узлов интерполяции. Возникает задача о наиболее рациональном выборе узлов 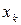так, чтобы полином 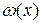имел наименьшее максимальное по модулю значение на отрезке [a,b].

Эта задача была решена П.Л. Чебышевым, который доказал, что наилучший выбор узлов дается формулой

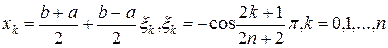(4.7)

- нули полинома Чебышева

Указания к выполнению лабораторной работы

1. Составить и отладить программу на функции, не имеющей никаких особых точек на отрезке интерполирования.

2. При исследовании точности для равномерной системы узлов и системы узлов Чебышева рассмотреть интерполирование указанной в вариантах заданий функции на различном числе узлов интерполяции. Сделать вывод о влиянии количества узлов на точность интерполяции.

3. При исследовании устойчивости интерполяции считать, что значения интерполируемой функции известны с какой-то случайной погрешностью. Сделать вывод о том, как эта случайная погрешность в узлах интерполяции влияет на значения полинома Лагранжа в промежуточных точках.

4. Предположим, что функция f(x) имеет особую точку 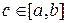. Тогда для оценки влияния особой точки c на точность и устойчивость следует рассматривать интерполяцию функции f(x) на интервале 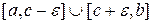, 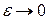. Оценить точность и устойчивость интерполяции при различных значениях .

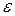5. Погрешность интерполяции оценить в метрике пространства C[a;b]. Особо внимательно исследовать отклонение интерполяционного многочлена от функции вблизи особых точек.