Лабораторная работа №4
Варианты заданий
1. 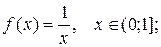
2. 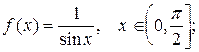
3. 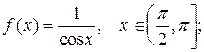
4. 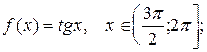
5. 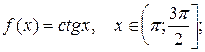
6. 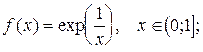
7. 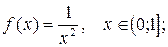
8. 
9. 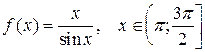 ;
;
10. 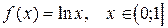 ;
;
11. 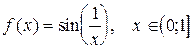 ;
;
12. 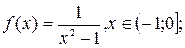
13. 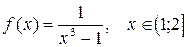 ;
;
14. 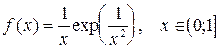 ;
;
15. 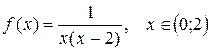 ;
;
16. 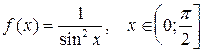 ;
;
17. 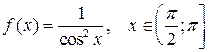 ;
;
18. 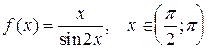 ;
;
19. 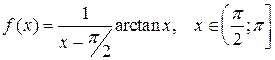 ;
;
20. 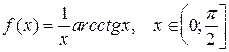 ;
;
21. 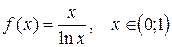 ;
;
22. 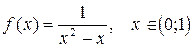 ;
;
23. 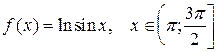 ;
;
24.  ;
;
25. 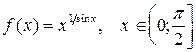 ;
;
Цель работы. Решение обыкновенного дифференциального уравнения первого порядка методами Рунге-Кутта.
Теоретическая часть
Пусть требуется найти на отрезке 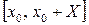 решение дифференциального уравнения
решение дифференциального уравнения
 (4.1)
(4.1)
Разобьем 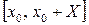 на отрезки
на отрезки 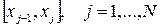 . Последовательно будем получать приближения
. Последовательно будем получать приближения 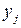 к значениям решения
к значениям решения 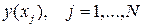 . Пусть значение
. Пусть значение 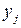 уже найдено, тогда значение
уже найдено, тогда значение 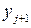 будем определять по следующей расчетной формуле
будем определять по следующей расчетной формуле
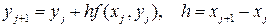 (4.2)
(4.2)
Этот метод называется методом Эйлера. Можно построить другой класс расчетных формул, к которому принадлежит метод Эйлера. Укажем сначала простейшие методы этого класса, получаемые из наглядных соображений. Пусть известно значение решения у(х) и требуется вычислить значение y(x+h). Рассмотрим равенство
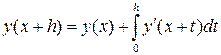 (4.3)
(4.3)
При замене интеграла в правой части на величину hy'(x) погрешность имеет порядок 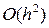 , т. е.
, т. е.
у (х + h) = у (х) + hу' (х) + О(h2);
поскольку у'(х) = f(x, y(x)), то отсюда имеем
y(x + h) = y(x) + hf (х, у (х)) + О (h 2).
Отбрасывая член порядка O(h2) и обозначая х =xj, x+h =xj +1, получим расчетную формулу Эйлера (4.2). Для получения более точной расчетной формулы нужно точнее аппроксимировать интеграл в правой части (4.3). Воспользовавшись формулой трапеций, получим
у (х + h) = у (х) +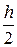 (у'(х) + у'(х + h)) + О (h3),
(у'(х) + у'(х + h)) + О (h3),
иначе,
y(x + h) = y(x) +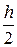 (f(x,y (x))+f(y+h, y (x+h))) +О (h3). (4.4)
(f(x,y (x))+f(y+h, y (x+h))) +О (h3). (4.4)
Соответствующая расчетная формула:
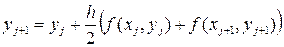 (4.5)
(4.5)
Обычно это уравнение неразрешимо явно относительно 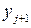 . Поэтому на практике чаще всего пользуются расчетными формулами
. Поэтому на практике чаще всего пользуются расчетными формулами
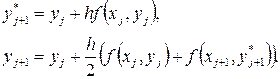 (4.6)
(4.6)
Если интеграл в правой части (4.3) заменить по формуле прямоугольников, то можно построить другую пару расчетных формул с погрешностью на шаге того же порядка:
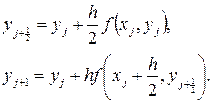 (4.7)
(4.7)
Полученные методы относятся к семейству методов Рунге-Кутта.
 2014-02-24
2014-02-24 357
357








