Внутренняя точка  интервала
интервала 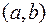 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если существует такое
, если существует такое 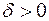 , что для всех
, что для всех 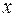 из интервала
из интервала 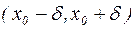 , содержащегося внутри интервала
, содержащегося внутри интервала 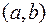 , выполняется неравенство
, выполняется неравенство
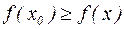 (
(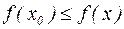 ).
).
Точки максимума и минимума называют точками экстремума (локального экстремума) функции. Точки, в которых производная обращается в ноль, называют стационарными точками. 
Приведем формулировки теорем, используемых при исследовании функций.
Достаточное условие строгого возрастания (убывания) функции: Если 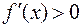 (
(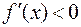 ) в интервале
) в интервале 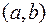 , то
, то 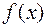 строго возрастает (убывает) в этом интервале.
строго возрастает (убывает) в этом интервале.
Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции необходимо:
1.найти область определения функции;
2.найти производную функции;
3.приравнять производную к нулю и определить ее корни (стационарные точки), а также найти точки, в которых производная не существует, а функция определена;
4. определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.
Необходимое условие экстремума функции: Если функция 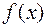 дифференцируема в точке
дифференцируема в точке  и достигает в этой точке максимума (минимума), то
и достигает в этой точке максимума (минимума), то 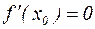 .
.
Точками экстремума могут быть только те точки, в которых производная равна нулю, либо не существует. Точки, в которых производная равна нулю или не существует, называют точками, подозрительными на экстремум, или критическими точками.
Достаточные условия экстремума функции: Если при переходе через точку  , подозрительную на экстремум, производная меняет знак, то точка
, подозрительную на экстремум, производная меняет знак, то точка  является точкой экстремума. При этом если в некоторой окрестности точки
является точкой экстремума. При этом если в некоторой окрестности точки 
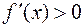 для
для 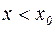 и
и 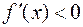 для
для 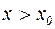 , то
, то  является точкой максимума. Если же в этой окрестности
является точкой максимума. Если же в этой окрестности 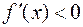 для
для 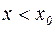 и
и 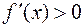 для
для 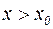 , то
, то  – точка минимума.
– точка минимума.
Другим достаточным признаком существования экстремума в стационарной точке  является условие
является условие 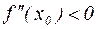 (тогда это точка максимума) и
(тогда это точка максимума) и 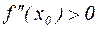 (тогда это точка минимума). При этом считается, что
(тогда это точка минимума). При этом считается, что  имеет непрерывную вторую производную в некоторой окрестности точки
имеет непрерывную вторую производную в некоторой окрестности точки  . Заметим, что
. Заметим, что 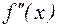 – вторая производная от функции
– вторая производная от функции  , полученная повторным дифференцированием этой функции:
, полученная повторным дифференцированием этой функции:
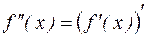 .
.
График функции 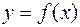 называется выпуклым вверх в интервале
называется выпуклым вверх в интервале 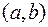 , если он расположен ниже касательной проведенной в любой точке этого интервала (рис.1)
, если он расположен ниже касательной проведенной в любой точке этого интервала (рис.1)
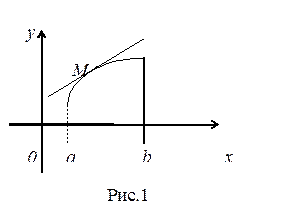
График функции 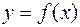 называется выпуклым вниз в интервале
называется выпуклым вниз в интервале 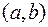 , если он расположен выше касательной, проведенной в любой точке этого интервала. (рис. 2)
, если он расположен выше касательной, проведенной в любой точке этого интервала. (рис. 2)
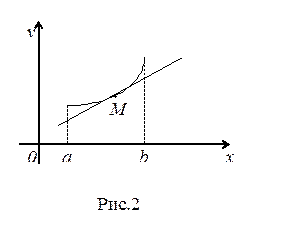
Достаточные условия выпуклости вверх (вниз) графика функции: Если 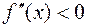 в интервале
в интервале 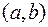 , то график функции является выпуклым вверх в этом интервале; если же
, то график функции является выпуклым вверх в этом интервале; если же 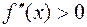 , то в интервале
, то в интервале 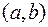 график функции является выпуклым вниз.
график функции является выпуклым вниз.
Точка 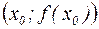 графика функции, переходя через которую график функции меняет характер выпуклости, называется точкой перегиба. Если
графика функции, переходя через которую график функции меняет характер выпуклости, называется точкой перегиба. Если  – абсцисса точки перегиба графика функции
– абсцисса точки перегиба графика функции 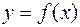 , то вторая производная равна нулю или не существует в этой точке. Точки, в которых
, то вторая производная равна нулю или не существует в этой точке. Точки, в которых 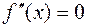 или
или 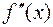 не существует, называются критическими точками второго рода.
не существует, называются критическими точками второго рода.
Если при переходе через критическую точку второго рода  вторая производная меняет знак, то точка
вторая производная меняет знак, то точка 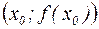 есть точка перегиба.
есть точка перегиба.
Прямая l называется асимптотой графика функции y = f(x), если расстояние от точки М(х,у) графика функции до прямой l стремится к нулю при неограниченном удалении этой точки от начала координат, (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Прямая 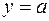 является вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов этой функции равен бесконечности:
является вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов этой функции равен бесконечности:
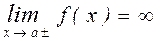 или
или 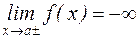 .
.
Вертикальные асимптоты следует искать в точках разрыва функции (в тех точках, в которых функция не определена).
Прямая 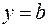 является горизонтальной асимптотой графика функции y = f(x), если существует предел функции равный b при
является горизонтальной асимптотой графика функции y = f(x), если существует предел функции равный b при 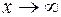 :
:
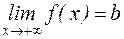
 или
или 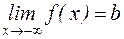
Прямая 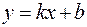 является наклонной асимптотой графика функции y = f(x), если существуют пределы:
является наклонной асимптотой графика функции y = f(x), если существуют пределы:
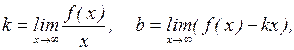
или 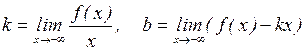 .
.
При исследовании функции и построении ее графика удобно придерживаться следующего плана:
1. Найти область определения функции.
2. Определить четность (нечетность), периодичность функции.
3. Найти точки разрыва.
4. Определить точки пересечения графика функции с осями координат.
5. Найти точки экстремума и вычислить значения функции в этих точках.
6. Определить интервалы возрастания и убывания функции.
7. Найти точки перегиба, интервалы выпуклости графика функции.
8. Определить асимптоты.
9. Найти предельные значения функции при аргументе, стремящемся к границам области определения.
В процессе исследования функции не обязательно строго придерживаться приведенной схемы.
Пример. Исследовать функцию 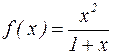 и построить ее график.
и построить ее график.
Решение: Данная функция определена и непрерывна на всей оси ОХ, за исключением точки 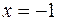 , где она терпит бесконечный разрыв.
, где она терпит бесконечный разрыв.
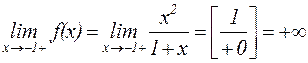
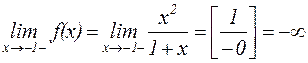
Следовательно, прямая 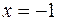 является вертикальной асимптотой. Справа от х = -1 график уходит вверх, а слева – вниз.
является вертикальной асимптотой. Справа от х = -1 график уходит вверх, а слева – вниз.
Поскольку 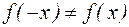 и
и 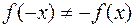 , то рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Точка (0,0) является точкой пересечения функции с осями координат.
, то рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Точка (0,0) является точкой пересечения функции с осями координат.
Вычислим производную:
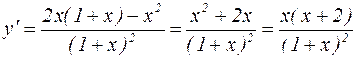 .
.
Производная обращается в нуль при 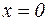 и
и 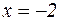 .
.
Построим интервалы монотонности (рис. 3):

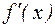 + _ _ +
+ _ _ +





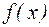 -2 -1 0 х
-2 -1 0 х
Рис. 3
Функция возрастает при 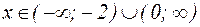 и убывает при
и убывает при 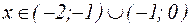 . Точка
. Точка 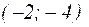 – точка максимума, а точка
– точка максимума, а точка 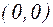 – точка минимума функции.
– точка минимума функции.
Найдем вторую производную:
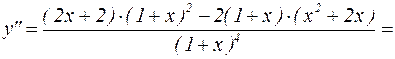
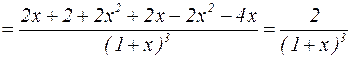 .
.
Вторая производная в нуль нигде не обращается, но при переходе через точку 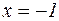 меняет свой знак с минуса на плюс. Следовательно, в интервале
меняет свой знак с минуса на плюс. Следовательно, в интервале 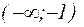 график функции выпуклый вверх, а в интервале
график функции выпуклый вверх, а в интервале 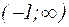 – выпуклый вниз. Точек перегиба функция не имеет.
– выпуклый вниз. Точек перегиба функция не имеет.
Выясним, имеет ли функция наклонные асимптоты.
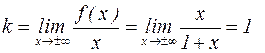 ,
,
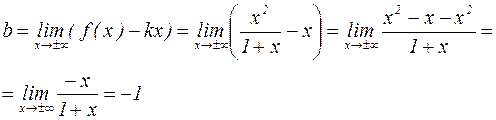
Следовательно, прямая 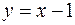 является наклонной асимптотой при
является наклонной асимптотой при 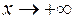 и при
и при 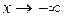 .
.
Построим график исследуемой функции:
Рис. 4
 2015-02-04
2015-02-04 409
409








