2014-02-24
566
Но не всегда уравнения решаются так просто. Рассмотрим следующий пример: решить уравнение √x = x - 2. Возводим по аналогии обе части этого уравнения в квадрат. Получаем x = x^2 - 4*x + 4.
Приводим подобные слагаемые и получаем следующее квадратное уравнение x^2 - 5*x - 4 = 0. Решаем это уравнение любым из известных способов, получаем два корня x = 1 и x = 4. Подставим эти корни в наше исходное уравнение, тем самым выполним проверку.
√4 = 4 - 2.
Получилось верное равенство следовательно х = 4 является корнем этого уравнения. Подставляем 1:
√1 = -1. В левой части получили отрицательное число -1, а в правой единицу. Равенство не выполняется. Следовательно, х = 1 не является корнем этого уравнения.
Ответ: х = 4.
Таким образом, мы убедились, что при решении иррациональных уравнений могут получиться побочные корни. И все решения полученные решения необходимо проверять.
Также уравнение может не иметь решений. Например, следующее уравнение √(x - 6) = √(4 - x) при решении дает один корень: х = 5. Но если его подставить, то не получится верного равенства. Следовательно, данное уравнение не имеет решений.
|
|
|
Бывают случаи, когда удобнее не подставлять полученные корни, а сразу решать уравнение, используя равносильные переходы. Пример: решить уравнение √(x - 2) = x - 8
По определению √(x - 2) не может быть отрицательным числом. Следовательно, и правая часть уравнения не может быть отрицательной. Тогда исходное уравнение равносильно следующей системе:
{ x - 2 = (x - 8)^2
{ x - 8 > = 0.
Решим первое уравнение системы. Оно будет равносильно квадратному уравнению x^2 -17*x + 66 = 0. Решив его, получим корни х = 11 и x = 6. Условие, записанное во втором неравенстве системы, будет выполнено только для корня х = 11. Следовательно, это и будет ответом уравнения.
Ответ: х = 11.
Иррациональные неравенства первого типа: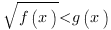 
Заметим, что в левой части неравенства стоит квадратный корень, который принимает только неотрицательные значения, следовательно, чтобы неравенство имело решения, правая часть должна быть положительной.
Получаем первое условие: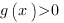 
Чтобы решить неравенство, нам нужно обе части возвести в квадрат.
Получаем второе условие: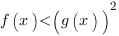 
Возведение в квадрат может привести к появлению посторонних корней, поэтому не забываем про ОДЗ: подкоренное выражение должно быть неотрицательным.
Получили третье условие: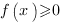 
Итак, неравенство вида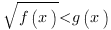 равносильно системе неравенств:
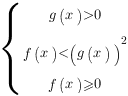
Аналогично, нестрогое неравенство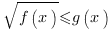 
равносильно системе неравенств:
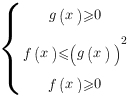
Иррациональные неравенства второго типа: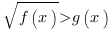 
.
Не смотря на то, что это неравенство с виду похоже на неравенство первого типа, оно принципиально от него отличается.
|
|
|
Поскольку в левой части неравенства стоит квадратный корень, левая часть всегда неотрицательна, поэтому
- если
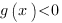
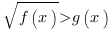, то неравенство выполняется при любом допустимом значении x, то есть при 
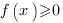. - если
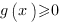, то мы можем обе части неравенства возвести в квадрат, получим 
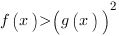, и условие на ОДЗ 
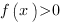будет автоматически следовать из этого неравенства.
Итак, неравенство вида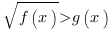 равносильно совокупности двух систем неравенств:
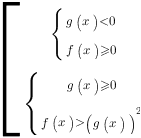
Нестрогое неравенство вида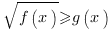 
равносильно совокупности:
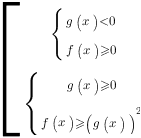
Рассмотрим примеры решения иррациональных неравенств.
1. Решить неравенство:
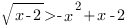
Это неравенство второго типа, оно равносильно совокупности двух систем:
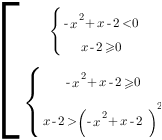
Решим каждое неравенство:
1. 
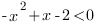
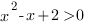
D=1-8=-7, старший коэффициент больше нуля, следовательно это неравенство верно при любом значении х. Решением первой системы будет решение ее второго неравенства: x≥2.
2. 
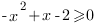Очевидно, что это неравенство не имеет решений. Следовательно, и вся вторая система не имеет решений.
Ответ: x≥2.
2. Решить неравенство:
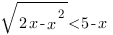
Это иррациональное неравенство первого типа, и оно равносильно системе трех неравенств:
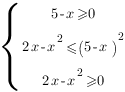
Решим каждое неравенство:
1. 
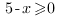
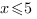
2. 
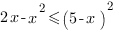
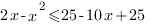
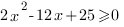
D=144-200<0, следовательно, это неравенство верно при любом значении х.
3. 
, 
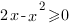
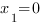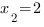
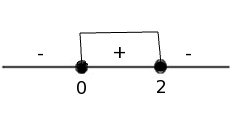Совместим решения первого и третьего неравенств системы на одной координатной прямой:
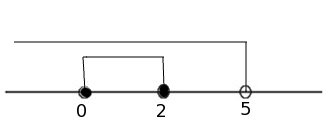Ответ: 0≤ x ≤ 2.
1000x=100
Представим левую и правую часть уравнения в виде степени, имеющую одинаковые основания:
103x=102
Теперь, когда основания одинаковые, нужно приравнять показатели степеней.
3x=2
x=2/3
Ответ: x=2/3.
Главное в показательных уравнениях - свести левую и правую часть уравнения к общему основанию:
