Раздел 2.
Глава 3. Векторная алгебра
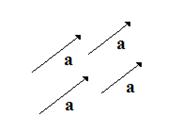
Вектором называется направленный отрезок прямой. Из определения следует, что вектор имеет три характеристики: прямую на которой он лежит, направление по прямой и длину. Первые две характеристики объединяются одним понятием – направление. Обозначаются вектора по точкам начала и конца АВ или 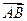 . Различают три вида векторов: свободные вектора, которые не меняются при параллельном переносе, вектора, которые можно переносить только по прямой на которой они лежат (например, вектора сил в механике) и радиус вектора, начало которых всегда находится в начале координат. Мы будем рассматривать только свободные вектора. Свободные вектора называют равными, если они лежат на одной или параллельных прямых, направлены в одну сторону и имеют одинаковую длину (рис 3.1), т. е. параллельный перенос вектора не меняет. Свободные вектора обозначают одной буквой
. Различают три вида векторов: свободные вектора, которые не меняются при параллельном переносе, вектора, которые можно переносить только по прямой на которой они лежат (например, вектора сил в механике) и радиус вектора, начало которых всегда находится в начале координат. Мы будем рассматривать только свободные вектора. Свободные вектора называют равными, если они лежат на одной или параллельных прямых, направлены в одну сторону и имеют одинаковую длину (рис 3.1), т. е. параллельный перенос вектора не меняет. Свободные вектора обозначают одной буквой 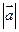 или а, b и т. д. Длину вектора обозначают при помощи модульных скобок
или а, b и т. д. Длину вектора обозначают при помощи модульных скобок 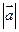 = ç а ç= а.
= ç а ç= а.
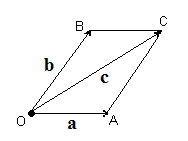
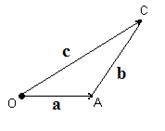
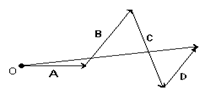
Вектора складывают по правилу параллелограмма: совмещают концы векторов, строят на векторах как на сторонах параллелограмм; суммой векторов называют вектор диагонали исходящий их общего начала a + b = c (рис.3.2). Вектора можно складывать и по правилу треугольника (рис. 3.3). Правило треугольника можно применить к сумме любого числа векторов (рис 3.4)
| |||
| |||
Умножение вектора на число λ идет по следующему правилу: при умножении на положительное число направление вектора сохраняется, при умножении на отрицательное – меняется на противоположное, а длина определяется по правилу (рис 3.5).
çλ а ç = 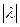 а (3.2)
а (3.2)
По определению a - b = a + (-1) b.
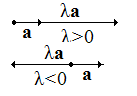
|
| ||||
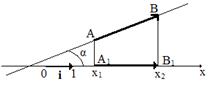
Проекцией вектора на ось ОХ называется число равноеразности координат проекций конца и начала вектора
prOX AB = x2 – x 1= ç AB çcos(α), (3.6)
где α - угол между вектором и осью (рис. 3.6).
Аналогично можно ввести проекцию вектора на оси OY и OZ:
prOY AB = y2 – y1= ç AB çcos(β) (3.6)
и
prOZ AB = z2 – z1= ç AB çcos(γ), (3.7)
где β и γ углы между вектором АВ и осями OY и OZ. Косинусы углов cos(α), cos(β) и cos(γ) называют направляющими косинусами
cos2(α)+cos2(β)+cos2(γ) = 1. (3.8)

|
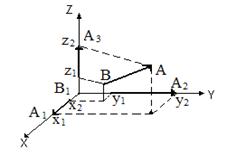
Если ввести i, j и k - единичные вектора осей ОХ, OY и OZ (их называют ортами), то вектор
A1B 1 = i( x2 – x1), A2B 2 = j (y2 – y1) и A3B 3 = k (z2 – z1). (3.9)
По правилу сложения векторов (рис. 3.7):
AB = A1B 1 + A2B 2 + A3B 3 = i( x2 – x1) + j (y2 – y1) + k (z2 – z1) ≡{ ( x2 – x1), (y2 – y1), (z2 – z1)}.
Равенство
AB = { ( x2 – x1), (y2 – y1), (z2 – z1)}(3.10)
называется «запись вектора в форме проекций».
Операции с векторами a, b заданными в форме проекций идут по следующему правилу:
a = {x1, y1, z1)}; b = {x2, y2, z2}
a + b = { (x1+x2), (y1 + y2), (z1 + z2)}; (3.11)
λ a = {λx1, λ y1, λz1}. (3.12)
Скалярным произведением векторов a = {x1, y1, z1)}; b = {x2, y2, z2} называют число равное произведению длин векторов на косинус угла между ними
а × b = (a,b) = ç a ç· ç b çcos(Ð a, b) = x1 x2 + y1 y2 + z1z2. (3.13)
Скалярное произведение перестановочно: а × b = b × а. Если вектора перпендикулярны, то скалярное произведение равно нулю. Скалярное произведение векторов используют для определения длины вектора
а × a = x1x1+ y1y1 + z1z1 = x12+ y12 + z12 Þ ç a ç= 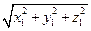 (3.14)
(3.14)
Замечание: скалярное произведение обозначается знаком 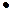 .
.
Пример. Найти угол φ между векторами 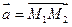 и
и 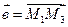 , если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
, если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
Решение. Для нахождения cosφ используем формулу
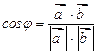
где 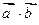 - скалярное произведение векторов
- скалярное произведение векторов 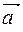 и
и 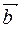 .
.
Определим координаты векторов 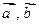 и cosφ:
и cosφ:
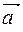 = (-3-1, 1+2, 1+3) =(-4, 3, 4),
= (-3-1, 1+2, 1+3) =(-4, 3, 4), 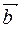 = (3-1, 2+2, 2+3) = (2, 4, 5),
= (3-1, 2+2, 2+3) = (2, 4, 5),
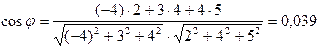 ,
,
φ = 87045'54".
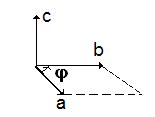
Векторным произведением векторов a и b называют такой вектор c = a ´ b, который:
1. лежит на прямой перпендикулярной плоскости векторов a и b,
2. имеет длину численно равную произведению длин векторов на синус угла между ними
ç c ç = ç a ç· ç b çsin(Ð a, b) = ç a ç· ç b ç sin(φ),
3. направление вектора c определяется по правилу буравчика: если вращать рукоять буравчика от первого вектора ко второму по наименьшему углу, то поступательное движение буравчика показывает направление вектора c.

Векторное произведение единичных векторов осей координат - ортов i, j, k равно
k = i ´ j, i = j ´ k, j = k ´ i. (3.15)
Векторное произведение не перестановочно: a ´ b = - b ´ a. Для коллинеарных векторов (лежащих на одной прямой) векторное произведение равно нулю a ´ b = 0, если a çç b. Для векторов заданных в форме проекций
с = a ´ b = 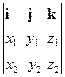 = i (y1z2 – y2z1) - j (x1z2 – z1x2) + k (x1y2 – x2y1). (3.16)
= i (y1z2 – y2z1) - j (x1z2 – z1x2) + k (x1y2 – x2y1). (3.16)
Длина вектора векторного произведение численно равна площади параллелограмма, построенного на векторах, как на сторонах: S = ç a ç ç b çsin(φ).
Замечание: векторное произведение обозначается знаком 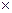 .
.
Смешанным произведением векторов a, b и c называется векторно-скалярное произведение
a ´ b × c = a × b ´ c º a b c = 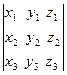 , (3.17)
, (3.17)
т. е. два вектора (первый – второй или второй – третий) перемножаются векторно, а третий вектор умножают на результат векторного произведения скалярно. В записи смешанного произведения знаки произведений обычно опускают. Смешанное произведение равно нулю, если векторы компланарны (лежат в одной плоскости). Смешанное произведение используют для вычисления объема параллелепипеда и пирамиды, построенной на векторах a, b, c.
Vпар = ê a b c ê; Vпир = 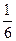 ê a b c ê.
ê a b c ê.
Пример. Даны координаты вершин пирамиды А1(1, -2, -3), А2(-3, 1, 1), А3(4, 3, -1), А4(3, 2, 2). Найти площадь грани А1 А2 А3 и объем пирамиды.
Решение. Площадь треугольника А1А2А3 найдем, используя геометрический смысл векторного произведения векторов
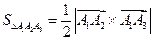 ,
,
где 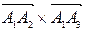 - векторное произведение векторов.
- векторное произведение векторов.
Вначале находим 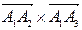
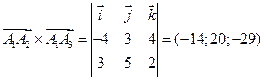 ,
,
а затем
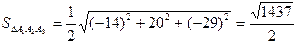 ед2.
ед2.
Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
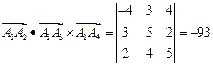 ,
,
следовательно, 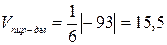 ед3.
ед3.
 2014-02-24
2014-02-24 929
929







