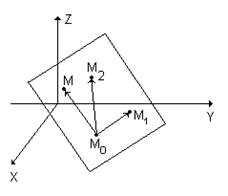
Из геометрии известно, что через три точки M0, M1 и M2 можно провести плоскость, причем единственным образом. Следовательно, добавив произвольную (текущую) точку плоскости М, можем построить три вектора М0М, М0М1 и М0М2, принадлежащих плоскости L. Смешанное произведение таких векторов равно нулю
М0М М0 М1 М0 М2 = 0, (2.3)
или, в развернутой форме,
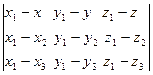 =0. (2.4)
=0. (2.4)
Это уравнение плоскости, проходящей через три данные точки.

П
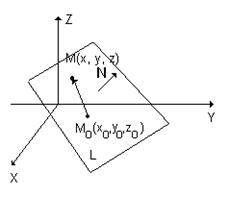
Плоскость L в пространстве можно задать единственным образом, если известна точка M0(x0,y0,z0), принадлежащая плоскости, и перпендикулярный плоскости вектор
N = { A, В, С}.
Если взять любую произвольную (текущую) точку плоскости M(x, y, z) и построить вектор М0М 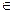 L, то векторы N и М0М перпендикулярны, т. е. их скалярное произведение равно нулю
L, то векторы N и М0М перпендикулярны, т. е. их скалярное произведение равно нулю
N × М0М =0 Þ A(x – x0) + B(y – y0) + C(z – z0) = 0. (2.5)
Это уравнение называется «уравнение плоскости, проходящей через данную точку».
Все уравнения плоскости можно свести к виду
Ax + By + Cz + D = 0. (2.6)
Это уравнение, линейное относительно всех неизвестных, называется общим уравнением плоскости в пространстве. Если D = 0, то уравнение Ax + By + Cz = 0 описывает плоскость, проходящую через начало координат.
Прямую в пространстве задаем как линию пересечения двух плоскостей. Общее уравнение прямой
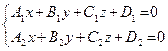 (2.7)
(2.7)
Если заданы точка М0, лежащая на прямой, и параллельный прямой вектор
S = {m, n, p},
то взяв текущую точку прямой М, постоим лежащий на прямой вектор М0 М.
Векторы М0 М и S параллельны, следовательно пропорциональны их проекции на оси координат
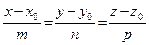 . (2.8)
. (2.8)
Это уравнение называется каноническим.
Пример. Даны координаты вершин пирамиды
А 1(1,-2,-3), А 2(-3,1,1), А 3(4,3,-1), А 4(3,2,2).
Составить: 1. Уравнение плоскости 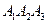 ,
,
2. Уравнение перпендикуляра, опущенного из вершины А 4 на грань 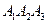 .
.
Решение. 1. Уравнение плоскости запишем, используя каноническое уравнение плоскости, проходящей через три данные точки:
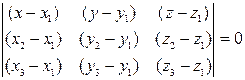 .
.
Подставив координаты точек А 1, А 2, А 3, получим
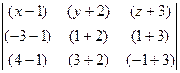 =
= 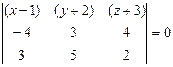
Разложив последний определитель по элементам первой строки, будем иметь
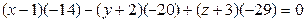
или
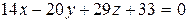 .
.
2.Уравнение высоты пирамиды представим в виде канонической системы уравнений прямой, проходящей через заданную точку А 4 с известным направляющим вектором 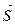 . За направляющий вектор
. За направляющий вектор 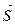 возьмем нормальный вектор
возьмем нормальный вектор 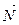 плоскости
плоскости 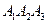 , т.е.
, т.е. 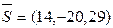 .
.
Уравнение высоты: 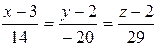 .
.
Примечание. Если бы в уравнении прямой один из знаменателей оказался нулевым, например
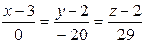 ,
,
то уравнение прямой следовало бы записать в виде пересекающейся системы плоскостей
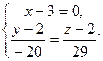
Наконец, если бы в уравнении прямой два знаменателя обратились в ноль, например,
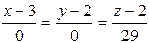 ,
,
это означало бы, что прямая является пересечением плоскостей 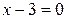 и
и 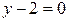 и ее уравнением будет система
и ее уравнением будет система
 2014-02-24
2014-02-24 1234
1234