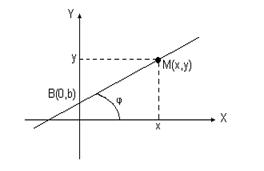
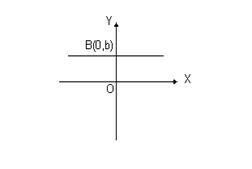
Пусть прямая линия пересекает ось ординат в точке B(0, b) под углом j к оси абсцисс (см. рис.1.5.а). Выберем на прямой произвольную точку M(x,y) (такая точка называется текущей). Проекции направленного отрезка BM на оси координат соответственно равны прхBM = х, пруBM = y - b. При скольжении точки M по прямой проекции изменяются, однако, их отношение, равное
tg j =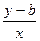 = k (1.8)
= k (1.8)
сохраняется для всех точек прямой и не выполняется для точек не принадлежащих прямой. Тангенс угла φ называется угловым коэффициентом и обозначается k.
|

Выразив из (1.8) y, получим " уравнение прямой линии с угловым коэффициентом"
у = х tgj + b или у= kх + b. (1.9)
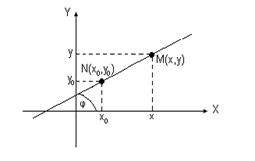
Если b=0, то прямая проходит через начало координат. Если k = 0, то прямая проходит параллельно оси абсцисс и ее уравнение у = b. Если вместо точки В дана другая фиксированная точка N(x0,y0) (рис. 1.5 б), то
k = tg j =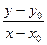
или
y – y0 = k(x – x0) (1.10)
Уравнение (1.10) называется "уравнение прямой, проходящей через данную точку". Если даны координаты двух точек N(x0,y0) и M(x1,y1), через которые проходит прямая, то
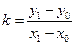
и уравнение
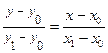 (1.11)
(1.11)
называется "уравнение прямой, проходящей через две данные точки"
,
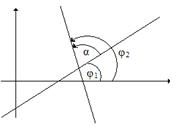

Угол α между двумя прямыми с угловыми коэффициентами k1 =tg(φ1) и k2= tg(φ2) (рис 1.6). Так как α = φ2 – φ1, то по формулам тригонометрии
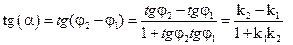 (1.12)
(1.12)
Условие параллельности прямых: k1=k2;
Условие перпендикулярности прямых 1= - k1 k2.
Любое из уравнений прямой можно привести к виду Ах + By + С = 0. Например, для уравнения (1.9) A =k, B = -1, C = b, т.е. прямая в прямоугольной системе координат может быть описана линейным уравнением первой степени. Если В 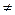 0, то уравнение
0, то уравнение
Ах + By + С = 0
можно привести к виду (1.9)
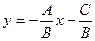 , k =
, k = 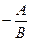 , b =
, b = 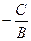 .
.

Если А = 0, то у = 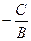 (рис. 1.7 а).
(рис. 1.7 а).
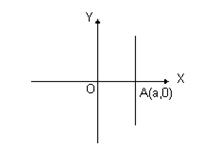
Если В = 0, то получим уравнение Ах + С = 0 или x = -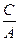 . Это уравнение определяет прямую параллельную оси ординат и пересекающую ось абсцисс в точке х = а (а = -
. Это уравнение определяет прямую параллельную оси ординат и пересекающую ось абсцисс в точке х = а (а = - 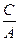 ) (рис. 1.7.б).
) (рис. 1.7.б).
Уравнение
Ах + Ву + С = 0. (1.13)
описывает только прямые линии на плоскости и называется общим уравнением прямой на плоскости. Верно и обратное утверждение: каждому уравнению первой степени с двумя неизвестными соответствует в прямоугольной системе координат одна и только одна прямая.
Если даны координаты концов отрезка А(х1, у1) и В(х2, у2), то координаты середины отрезка тоски С (х3, у3) находятся по формуле
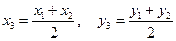 (1.14)
(1.14)
Пример. Даны две вершины треугольника А (-3,-3) и С (5,1); его биссектрисы пересекаются в точке N (2,2). Найти координаты вершины В и уравнение медианы, проведенной из этой вершины.
Решение. Для нахождения дополнительных точек на сторонах АВ и ВС будем использовать геометрическое свойство биссектрис AN и CN.
1. Составляем уравнение биссектрис AN и CN:
2.
уравнение AN: 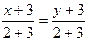 или
или 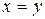 ,
,
уравнение CN: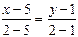 или
или 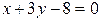 .
.
2. Далее рассуждаем так: AN – биссектриса угла А, поэтому на стороне АВ должна лежать точка С 1, симметричная точке С относительно AN. Аналогично на стороне ВС должна найтись точка А 1, симметричная точке A относительно биссектрисы CN. Найдем точки С 1 и А 1.
Составляем уравнение перпендикуляра CF, опущенного из вершины С на биссектрису АN:
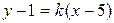 , где
, где 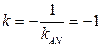 .
.
Следовательно, уравнение CF: 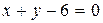 .
.
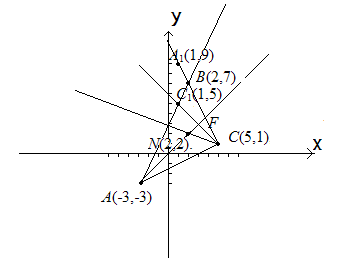
Рис. 1.8.
Находим координаты точки F пересечения AN и перпендикуляра CF, решая систему
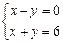
откуда F (3,3).
Определяем координаты точки С 1, учитывая, что отрезок С 1 С в точке F делится пополам и, следовательно,
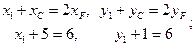
или С 1(1,5).
Поступая аналогично, находим точку А 1(1,9).
Составляем уравнения сторон АВ и ВС, соответственно,
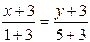 и
и 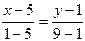
Или
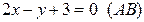 и
и 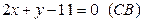 .
.
Находим координаты вершины В, решая систему
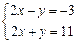
из которой следует, что В (2,7).
5. Составляем уравнение медианы ВЕ, предварительно найдя координаты точки Е - середины стороны АС. Имеем
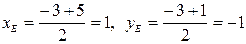 .
.
Уравнение ВЕ:
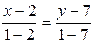 или
или 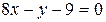 .
.
Кривые второго порядка.
Кривыми второго порядка называются линии, которые описываются алгебраическими уравнениями второй степени
Ax2 + B xy + C y2 + Dx + Ey + F = 0, (1.15)
причем хотя бы один из коэффициентов А, B, С должен быть не равен нулю.
Окружностью называется геометрическое место точек равноудаленных от данной точки, называемой центром окружности. Уравнение окружности радиуса R с центром в точке M(а,b) имеет вид
(x - a)2 + (y - b)2 = R2. (1.16)
Если раскрыть скобки, то мы увидим, что уравнение (1.16) получается из уравнения (1.15), если
A = C = 1, B=0, D =-2a, E = -2b, F = - R2 + a2 + b2.
Пример. Пусть задано уравнение х2 + y2 - 4x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра?
Попробуем привести данное уравнение к виду (1.16). Выделим полный квадрат относительно х, прибавляя и вычитая число 4
x2 + y2 - 4x = (x2 - 4x + 4) + y2 - 4 = 0
или
(x - 2)2 + y2 = 22. (1.17)
Сравнивая (1.16) с (1.17), видим, что заданное уравнение есть уравнение окружности радиусом R =2 и с центром в точке M(2,0).
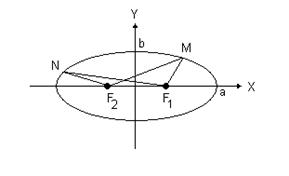
Эллипс - замкнутая кривая, для всех точек которой сумма расстояний до двух фиксированных точек F1 и F2, называемых фокусами эллипса, есть величина постоянная (т.е. одинакова) и равна, по определению, 2а (а>0).
Для эллипса, представленного на рис.1.9, сумма расстояний MF1 и MF2 равна сумме расстояний NF1 и NF2, т. е.
MF1 + MF2 = NF1 + NF2 = 2а,
причем
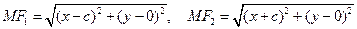 .
.
Уравнение эллипса, центр симметрии которого находится в начале координат, а фокусы F1 (с,0) и F2 (-с,0) лежат на оси ОХ симметрично относительно оси OY называется каноническим
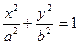 . (1.18)
. (1.18)
Параметры a и b называются полуосями эллипса (величины 2а и 2b называются осями), причем
a2 = b2+c2.
Отношение 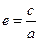 называется эксцентриситетом, эксцентриситет эллипса меньше единицы е < 1.
называется эксцентриситетом, эксцентриситет эллипса меньше единицы е < 1.
Уравнение (1.18) получим из (1.16) если
B = D = E = 0, 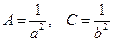 , F=-1.
, F=-1.
Очевидно, что окружность - частный случай эллипса, у которого a = b = R, а центр находится в начале координат.
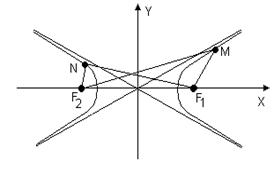

Гипербола – неограниченная кривая, для всех точек которой разность расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и по определению равна 2а (рис. 1.10).
Разность
MF2 – MF1 = NF1 – NF2 = 2а.
где
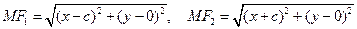 .
.
Каноническое уравнение гиперболы, центр симметрии которой совпадает с началом координат, а фокусы F1 и F2 лежат на оси OX симметрично оси OY
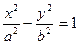 . (1.19)
. (1.19)
Параметры а и b называются полуосью и мнимой полуосью гиперболы, причем
c2=b2+a2.
Эксцентриситет гиперболы 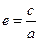 больше единицы e > 1.
больше единицы e > 1.
Уравнение (1.19) получим из (1.15) если
B = D = E = 0, 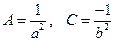 , F=-1.
, F=-1.
Особенность гиперболы – наличие асимптот - прямых к которым неограниченно приближается кривая при 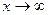 . Уравнения асимптот
. Уравнения асимптот
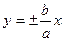 .
.
Парабола - неограниченная кривая, все точки которой (рис. 2.12) равноудалены от точки, называемой фокусом и прямой, называемой директрисой, причем расстояние между фокусом и директрисой равно р.
Для параболы изображенной на рис.1.11 расстояния MK = MF, NF = NL и DO =OF. Каноническое уравнение параболы, фокус которой F(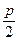 ,0) лежит на оси ОХ, а директриса х =
,0) лежит на оси ОХ, а директриса х = 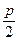 перпендикулярна ОХ, есть
перпендикулярна ОХ, есть
y2 = 2px, (1.20)
Уравнение (1.20) получим из (1.15) если
A = B = E = F = 0, C = 1, D = -2p.
Ось такой параболы совпадает с осью ОХ, а вершина лежит в начале координат.
Сделав поворот и сдвиг системы координат любое уравнение (1.15) можно привести только к одному из трех уравнений второй степени: (1.18), (1.19), (1.20) или к уравнению вида
а2 х2 = b2 y2 ,
которому соответствуют две прямые. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай окружность), гиперболу или параболу. Важным свойством линий второго порядка является то, что все они могут быть получены (см. рис. 1.12) как сечения конуса плоскостью, пересекающего его под различными углами.

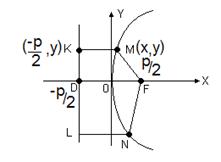
Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x 0, y 0) (случай В).
А В
| Окружность | 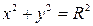
| 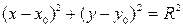
| |
| Эллипс | 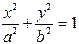
| 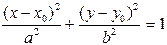
| |
| Гипербола | 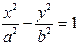
| 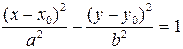
| |
| Парабола | 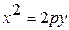
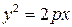
| 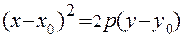 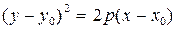
|
Пример. Найти геометрическое место точек разность квадратов расстояний которых от точек А(1, 2) и В(5, 3) равна 4.
Решение. Обозначим за М(x, y) текущую точку кривой. Тогда по условию
МА – МВ = 4.
В координатной форме
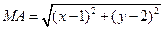 ,
, 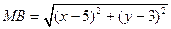 или
или
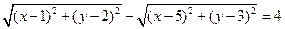 .
.
Перенесем второй корень направо и возведем в квадрат
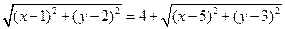
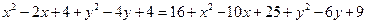
или 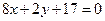 . Это уравнение прямой линии (рис. 1.13)
. Это уравнение прямой линии (рис. 1.13)
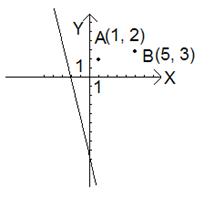
Рис. 1.13.
 2014-02-24
2014-02-24 1296
1296
