выполняют следующие шаги:
1. Ранжируют данные.
2. Строят статистический ряд.
3. Вычисляют теоретические вероятности попадания в каждый интервал группирования по формуле: 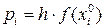 , где
, где 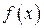 − плотность распределения вероятности и
− плотность распределения вероятности и 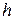 − длина интервала группирования количественного признака
− длина интервала группирования количественного признака 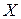 .
.
4. Вычисляют теоретические частоты по формуле: 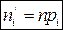 (округляя до целого).
(округляя до целого).
5. Задают уровень значимости 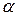 .
.
6. Определяют критическую точку (правосторонняя критическая область), исходя из условия 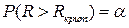 , и количества степеней свободы
, и количества степеней свободы 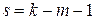 , где
, где 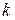 − количество интервалов группирования признака,
− количество интервалов группирования признака, 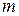 − количество параметров рассматриваемого распределения; например, для нормального распределения
− количество параметров рассматриваемого распределения; например, для нормального распределения 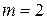 , т.к. оно определяется двумя параметрами – математическим ожиданием и средним квадратическим отклонением.
, т.к. оно определяется двумя параметрами – математическим ожиданием и средним квадратическим отклонением.
7. Вычисляют по выборке наблюдаемое значение критерия.
8. Если наблюдаемое значение больше критического, то гипотезу отвергают; в противном случае, нет оснований отвергнуть гипотезу (отвергают гипотезу более категорично, чем принимают).
В качестве критерия проверки статистических гипотез будем рассматривать критерий Пирсона 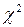 (хи-квадрат), который наиболее широко применяется для этой цели.
(хи-квадрат), который наиболее широко применяется для этой цели.
Для определения критических точек распределения 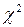 при различных уровнях значимости
при различных уровнях значимости 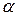 и степенях свободы
и степенях свободы 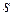 составлены специальные таблицы.
составлены специальные таблицы.
Определение. Наблюдаемым значением критерия Пирсона называется величина 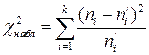 .
.
Пример. Для нашей выборки проверить гипотезу при уровне значимости 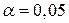 , если предположить, что количественный признак генеральной совокупности распределен нормально.
, если предположить, что количественный признак генеральной совокупности распределен нормально.
Решение.
Нормальное распределение имеет плотность 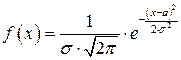 , полагая
, полагая 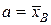 и
и 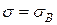 найдем теоретические вероятности по формуле
найдем теоретические вероятности по формуле 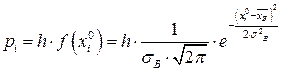 .
.
Теоретические вероятности (для проверки гипотезы о нормальном распределении количественного признака 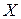 генеральной совокупности) можно так же вычислять по формуле
генеральной совокупности) можно так же вычислять по формуле 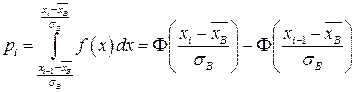 , где
, где 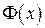 − функция стандартного нормального распределения.
− функция стандартного нормального распределения.
Вычисляют теоретические частоты по формуле: 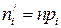 (округляя до целого).
(округляя до целого).
Наблюдаемым значением критерия Пирсона вычисляем по формуле 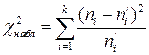 .
.
Занесем все данные в следующую таблицу:
Номер интер- вала
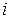
| Частоты пi | Теоретич. вероятности
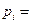 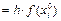
| Теоретич. частоты
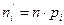
| Компоненты 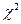
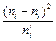
|
| 0,015 | ||||
| 0,070 | 0,33 | |||
| 0,192 | 0,4 | |||
| 0,296 | 0,07 | |||
| 0,258 | 0,08 | |||
| 0,127 | 0,17 | |||
| 0,035 | ||||
| 0,992 | 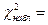 1,05 1,05
|
Наблюдаемое значение критерия равно: 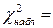 1,05. Число степеней свободы равно:
1,05. Число степеней свободы равно: 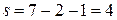 . По таблице находим:
. По таблице находим: 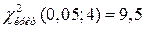 . Так как наблюдаемое значение критерия меньше, чем критическое (т.е. теоретическое значение), то делаем вывод, что нет оснований отвергнуть гипотезу о нормальном распределении.
. Так как наблюдаемое значение критерия меньше, чем критическое (т.е. теоретическое значение), то делаем вывод, что нет оснований отвергнуть гипотезу о нормальном распределении.
 2014-02-09
2014-02-09 313
313







