Приложения скалярного произведения
Свойства скалярного произведения.
Скалярное произведение векторов
Скалярным произведением двух векторов 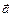 и и 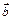 называется число называется число
 ,
где ,
где 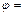
| |||||||||||||||||
|
| ||||||||||||||||
Нетрудно заметить (см. св-во проекции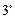 :
: ), что
), что
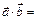
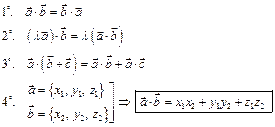
Д-во: 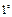 –
–
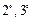 –
–
Используя свойства 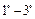 и полученные выше значения из таблицы, докажем св-во
и полученные выше значения из таблицы, докажем св-во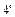 .
.
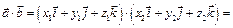
1. 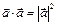 .
.
2. 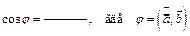 .
.
2а. 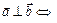
3. Известно, что работа постоянной силы 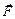 при перемещении при перемещении 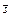 равна равна
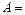 где
где 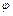 – угол между направлением перемещения и вектором силы, т.е. – угол между направлением перемещения и вектором силы, т.е.
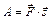 . .
|
Тройка некомпланарных (не лежащих в одной плоскости) векторов 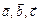 в указанном порядке образует правую тройку, если с конца третьего вектора
в указанном порядке образует правую тройку, если с конца третьего вектора 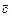 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 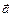 ко второму вектору
ко второму вектору 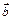 наблюдается против часовой стрелки. В противном случае тройка называется левой.
наблюдается против часовой стрелки. В противном случае тройка называется левой.
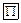 Определить ориентации троек:
Определить ориентации троек:
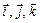 ;
; 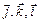 ;
; 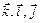
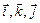 ;
; 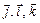 ;
; 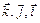
Векторным произведением 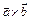 вектора
вектора 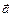 на вектор
на вектор 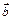 называется вектор
называется вектор 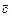 такой, что
такой, что
1. 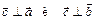 ;
;
2. тройка 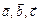 – правая;
– правая;
3. 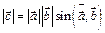 .
.
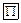 (строка
(строка 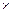 столбец)
столбец)
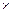
| 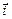
| 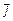
| 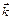
|
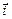
| |||
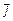
| |||
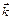
|
 2014-02-09
2014-02-09 455
455