2014-02-24
1538
Пусть есть последовательность дискретных отсчетов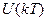 
.
Полином второй степени имеет вид:
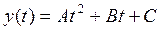(8.3)
На каждом интервале интерполяции, включающем два периода дискретизации, полином вида (8.3) проводится через три соседних отсчета (рисунок 8.3). При этом на каждом интервале интерполяции надо рассчитывать свои коэффициенты А, В, С.
Для нахождения коэффициентов полинома необходимо решить систему из трех уравнений:
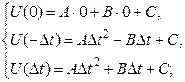(8.4)
В результате решения (8.4) получим выражения для определения коэффициентов:
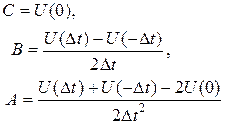
Рисунок 8.3 – Построение интерполирующей функции второго порядка
Интерполирующий многочлен Лагранжа
В качестве интерполирующего полинома при скользящем интерполировании часто применяется многочлен Лагранжа n -ной степени:
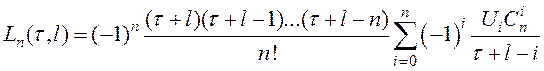, (8.5)
где l – интервал соответствия,
l =0, 1, 2,…, n -1; n – степень полинома,
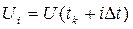– значения отсчетов внутри интервала интерполяции,
t k – начало интервала интерполяции,
i =0, 1,…, n – порядковый номер отсчета восстанавливаемой функции,
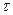– относительное время внутри интервала интерполяции,
|
|
|
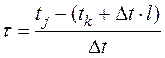, (8.6)
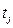- произвольный момент времени внутри интервала интерполяции.
Многочлен Лагранжа первой степени:
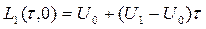
Индивидуальное задание. Вывести самостоятельно многочлены Лагранжа второй степени для l =0 и l =1 из общего выражения (8.5).
Погрешность интерполяции
Ограничение степени интерполирующего полинома приводит к погрешности интерполяции. В случае использования интерполирующего полинома Лагранжа максимальная погрешность интерполяции определяется остаточным членом для многочлена Лагранжа степени n:
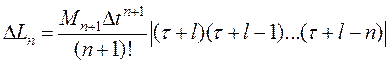(8.7)
где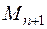 
- максимум n +1 производной восстанавливаемого сигнала.
В точках, совпадающих с отсчетами (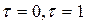
) погрешность интерполяции равна нулю, 
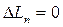. При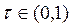 
погрешность не равна нулю, 
.
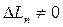Пусть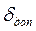 
– допустимая приведенная погрешность восстановления.
Зная диапазон изменения сигнала U макс, определим абсолютную допустимую погрешность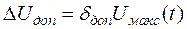 
.
Очевидно, что при восстановлении непрерывного сигнала должно выполняться условие: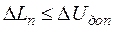 
. С учетом (8.7) это условие можно представить в виде
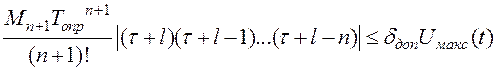. (8.8)
Здесь введено новое обозначение периода дискретизации - Т опр, то есть период опроса. Очевидно, что чем меньше период опроса, тем точнее может быть восстановлен непрерывный сигнал по дискретным отсчетам. Задавшись допустимой погрешностью восстановления, из (8.8) можно определить предельно допустимое максимальное значение периода опроса
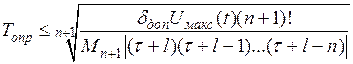. (8.9)
Выражение (8.9) справедливо для погрешностей восстановления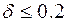 
.
В этом случае для интерполяции с использованием полиномов Лагранжа нулевого, первого и второго порядков, называемую также ступенчатой, линейной и параболической интерполяцией, справедливы выражения:
|
|
|
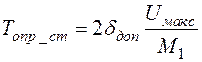, (8.10)
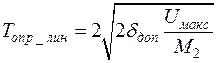, (8.11)
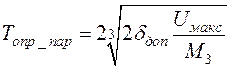. (8.12)
Последнее выражение справедливо как для l =0, так и для l =1.
Максимум (n +1)-й производной можно определить только для детерминированного сигнала, например гармонического. Для реальных сигналов невозможно определить M n+1.
Для сигнала с прямоугольным спектром получены следующие соотношения [Пенин П.И. Системы передачи цифровой информации]:
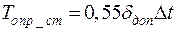(8.13)
или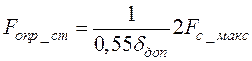 
, (8.14)
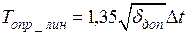(8.15)
или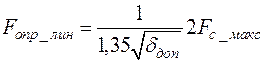 
, (8.16)
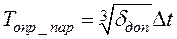, (8.17)
или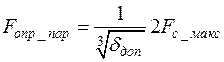 
, (8.18)
где Δ t – период дискретизации по теореме Котельникова,
F с макс – максимальная частота в спектре дискретизируемого сигнала.
